机器学习算法笔记(二十四)：决策边界

上一篇文章中我们简单的讨论了逻辑回归的基本原理以及算法的推导。本文我们在这个基础上引出一个对于分类问题来说非常重要的概念——决策边界(Decision Boundary)。

一、决策边界的基础理解

首先我们回顾一下上一篇文章中对于逻辑回归的基本概念：

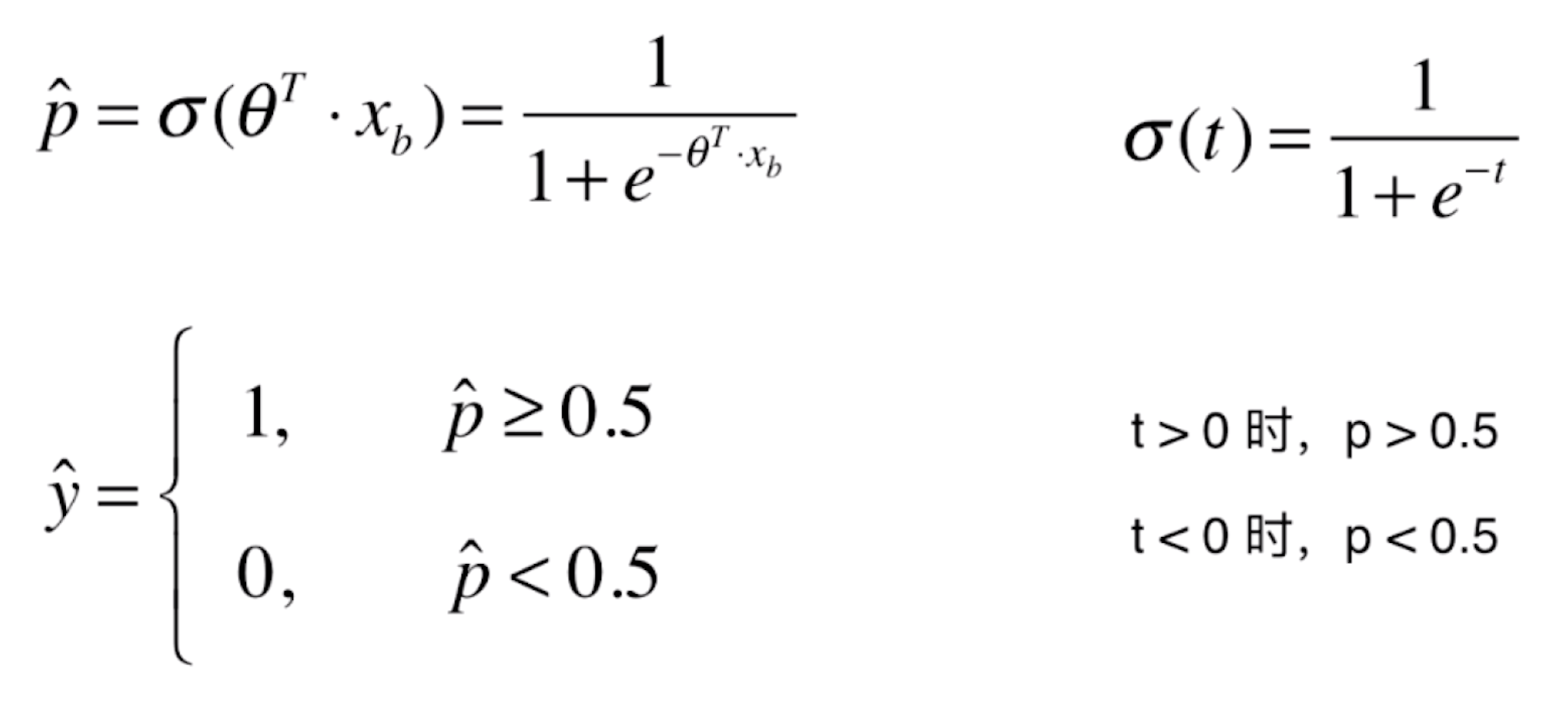
其中，由于 t=，所以进一步可以化为：

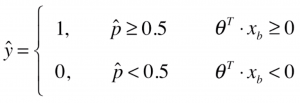
其中，大于0，我们将预测值设为1，反之设为0。换句话说，预测值是1还是0的边界点在于=0的位置，这个位置就被称作决策边界。

在特征空间内，根据不同特征对样本进行分类，不同类型间的分界就是模型针对该数据集的决策边界。通过决策边界可以更好的可视化分类结果。

二、编程绘制决策边界

=0时，我们假设它有两个特征，那么就有。这个式子显然是一个直线表达式。因为分类问题中特征空间的坐标轴都表示特征，我们把 x1 作为横轴特征，x2 作为纵轴特征，简单的转换一下，就有。下面我们就编程来绘制这条直线，在上一篇文章的代码最后，补充上以下代码：

import matplotlib.pyplot as plt

#x2()函数：求满足决策边界关系的直线的函数值
def x2(x1):
    return (-log_reg.coef_[0] * x1 - log_reg.intercept_) / log_reg.coef_[1]

x1_plot = np.linspace(4, 8, 1000) #在4至8之间取1000个点
x2_plot = x2(x1_plot)

plt.scatter(X[y==0,0], X[y==0,1], color="red")
plt.scatter(X[y==1,0], X[y==1,1], color="blue")
plt.plot(x1_plot, x2_plot)
plt.show()

绘制结果如下：

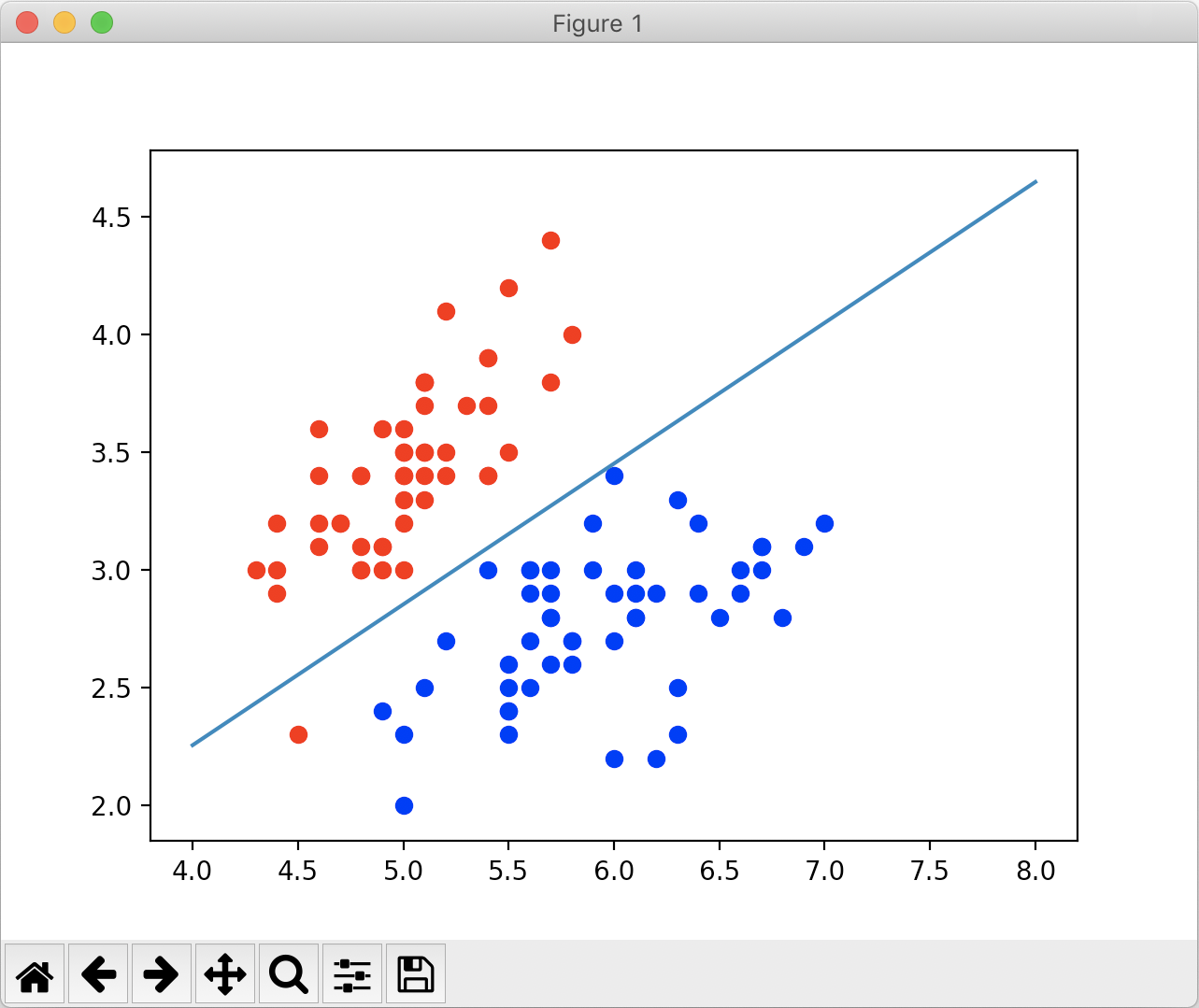
我们看到这根蓝色的直线就是所谓的决策边界，大体上把红色点和蓝色点分成了两部分。若新的样本在这根直线下面，就把它分类为1；若新样本在直线上面，就把它分类为0；若新样本正好落在直线上，此时我们将它分类成0和1都是可以的。

我们可以看到有一个红色的点和其他红点不在决策边界的一侧，显然这是一个分类错误的情况。

三、不规则的决策边界的绘制

通过上一节实验我们发现，逻辑回归算法得到的决策边界是一条直线，本质上还是线性回归的一种。那对于其他的不规则决策边界我们如何绘制呢？其实非常简单也比较笨：先通过细分将特征空间分割无数的点，对于每一个点都使用模型对其进行预测分类，并将这些预测结果绘制出来，不同颜色的点的边界就是分类的决策边界。

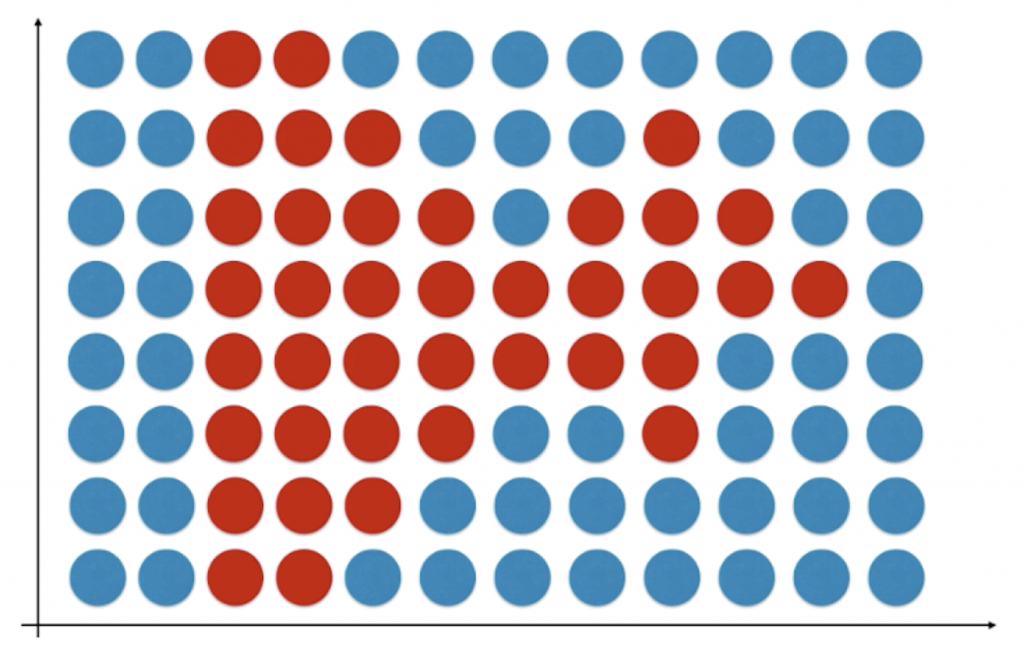
我们下面来尝试绘制逻辑回归的决策边界，在上面的代码中添加如下代码：

def plot_decision_boundary(model, axis):
    #model：算法模型
    #axis：区域坐标轴的范围，其中 0,1,2,3 分别对应 x 轴和 y 轴的范围
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1), #将x轴划分为无数小点
        np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1), #将y轴划分为无数小点
    )
    X_new = np.c_[x0.ravel(), x1.ravel()] #np.c_表示按列连接两个矩阵；ravel()函数用于将多维数组降至1维

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])

    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap) #绘制等高线，以标记作为等高线高度值


plot_decision_boundary(log_reg, axis=[4, 7.5, 1.5, 4.5])

#绘制数据集点
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])

plt.show()

绘制结果如下：

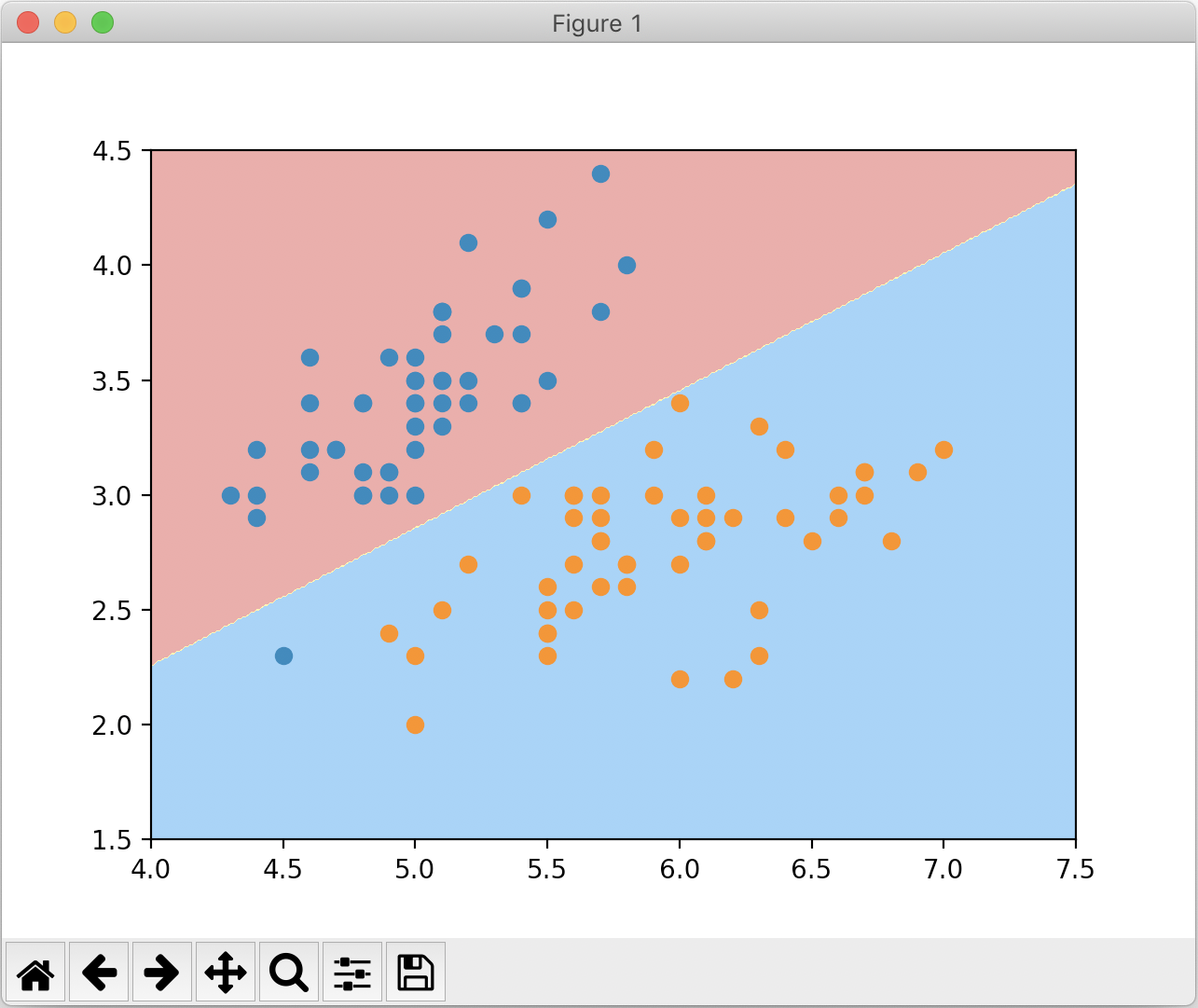
有了这个方法，我们就能用它来绘制kNN算法的决策边界，即便kNN算法的决策边界没有数学表达式。实现如下：

from sklearn.neighbors import KNeighborsClassifier

knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_train)

plot_decision_boundary(knn_clf, axis=[4, 7.5, 1.5, 4.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()

绘制的决策边界如下：

可以看到，使用默认k=5绘制出来的边界非常不规则，出现了过拟合的现象（k越小模型越复杂）。我们把k值换成50再次运行，结果如下：

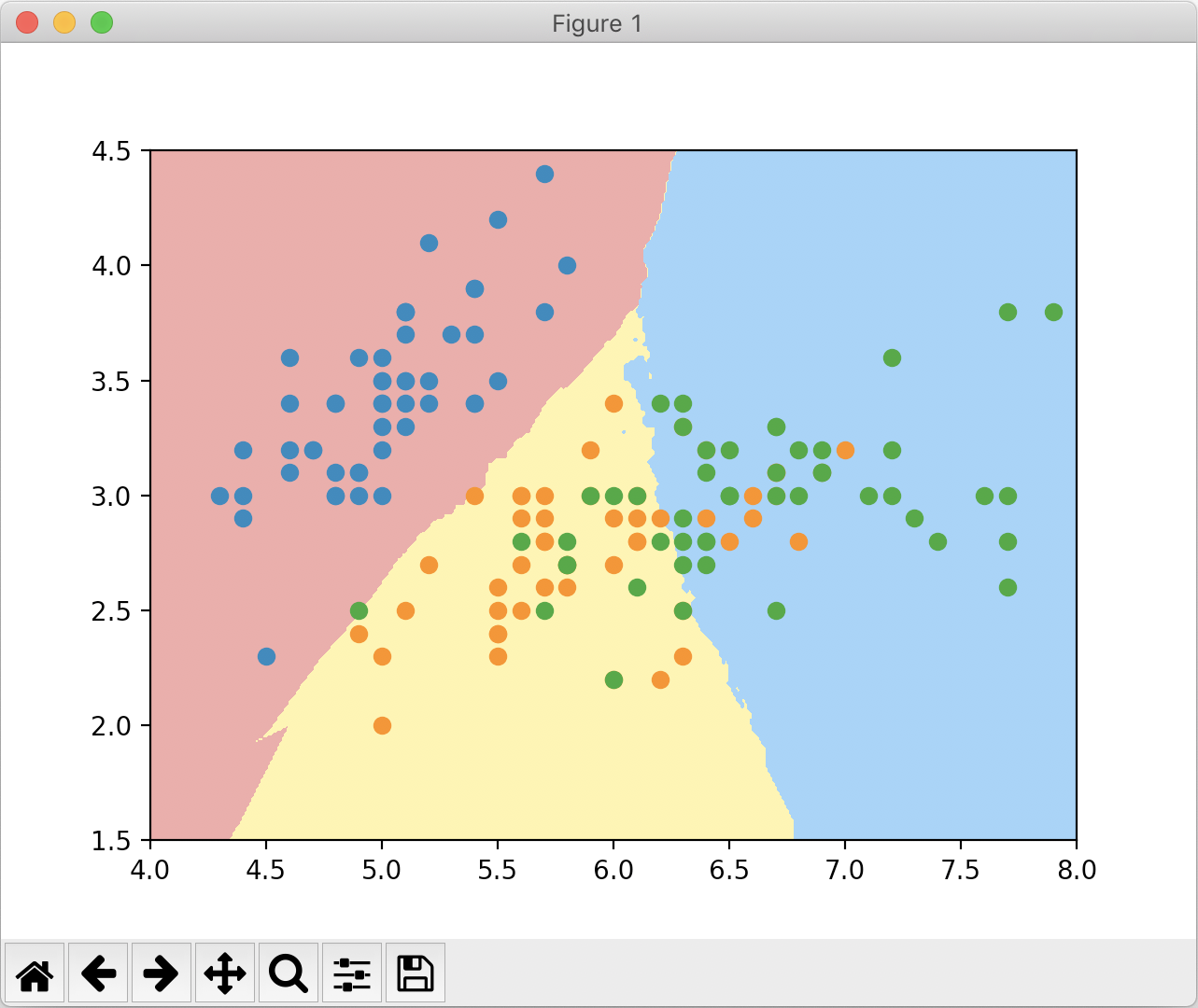
k=50时，得到的边界明显规整的多。

四、为逻辑回归添加多项式项

通过上面的讨论我们可以看出，逻辑回归中的决策边界本质上相当于在特征平面中找一条直线，用这条直线分割所有的样本对应的分类。这也说明了为什么逻辑回归只能处理二分类问题——一条直线只能将特征平面分成两部分（不算这条直线本身）。尽管如此，我们使用直线来分类还是太过简单了，显然在很多情况下不能将样本点很好分割成两部分。

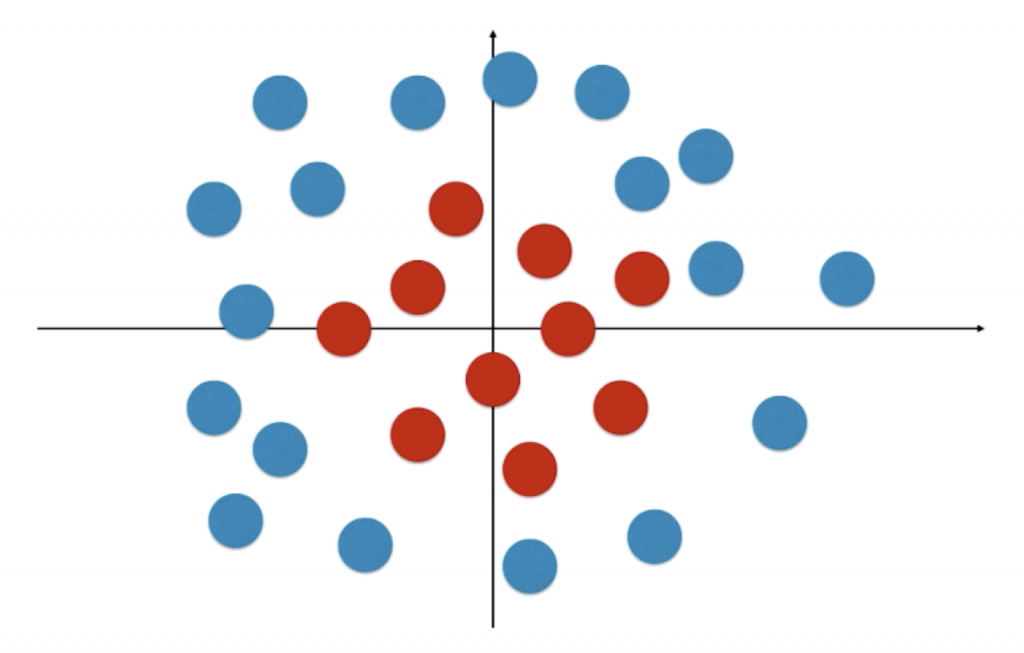
我们以上图为例，很明显对于这个样本来说，它的决策边界可以大致用一个圆心在原点的圆来表示。和多项式回归类似，我们只要在逻辑回归中引入多项式项（将 x1² 和 x2²整体看作一个特征），就能较好的表示非线性分布的决策边界。在上文的工程中新创建一个文件，实现如下代码：

import numpy as np
import matplotlib.pyplot as plt
from MyML.LogisticRegression import LogisticRegression


def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])

    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

#模拟创建上文图片实例的数据集
np.random.seed(666)
X = np.random.normal(0, 1, size=(200, 2))
y = np.array((X[:,0]**2+X[:,1]**2)<1.5, dtype='int')

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

def PolynomialLogisticRegression(degree):
    return Pipeline([
        ('poly', PolynomialFeatures(degree=degree)), #引入多项式项
        ('std_scaler', StandardScaler()),
        ('log_reg', LogisticRegression())
    ])

poly_log_reg = PolynomialLogisticRegression(degree=2) #引入2阶多项式
poly_log_reg.fit(X, y)
print(poly_log_reg.score(X, y)) #prints: 0.95

plot_decision_boundary(poly_log_reg, axis=[-4, 4, -4, 4])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()

绘制出的决策边界如下：

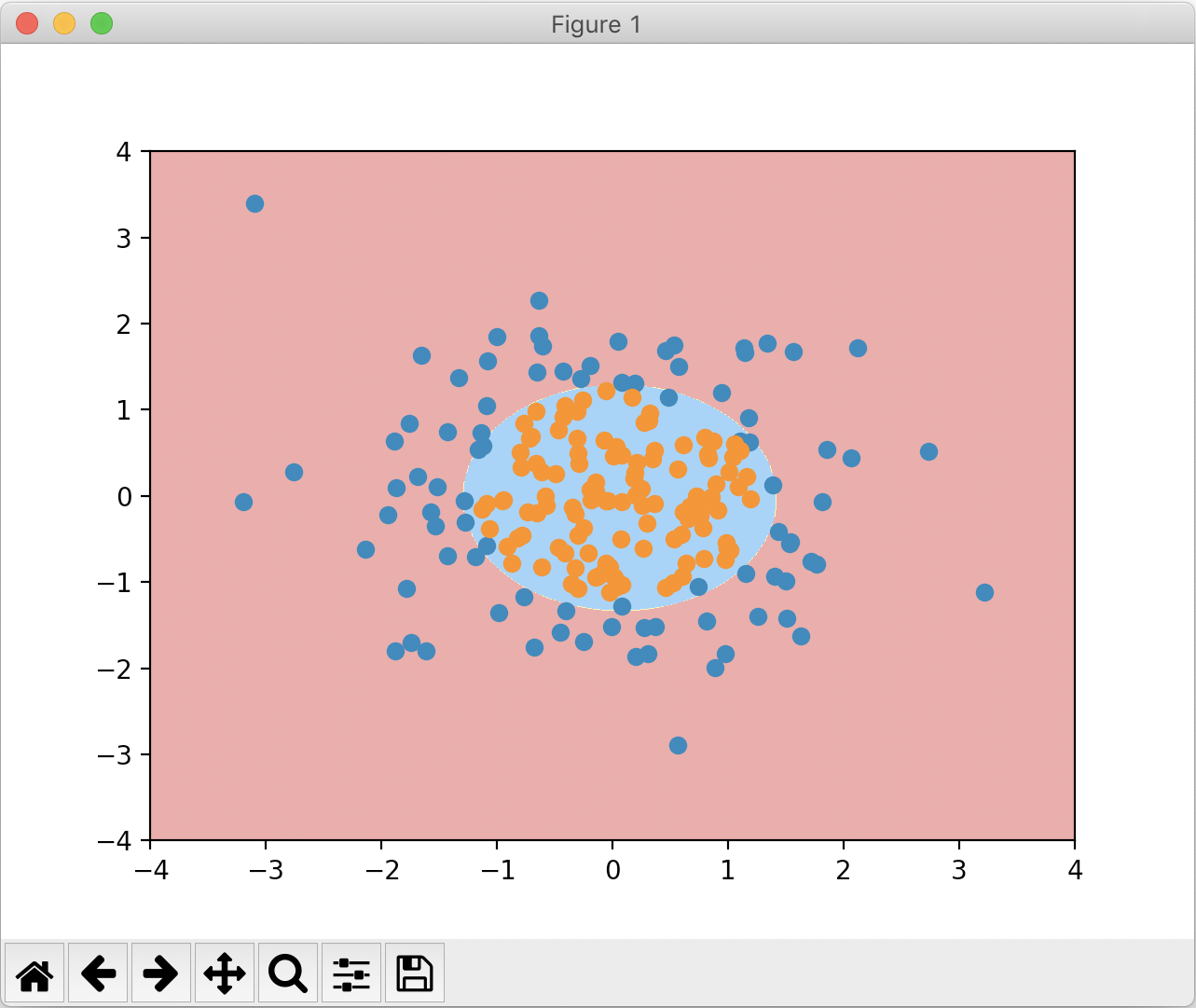
PolynomialLogisticRegression的degree值是一个超参数。如果degree过大，会导致过拟合的情况，选取degree值时需要特别注意。当然，我们更推荐使用模型正则化来解决逻辑回归中过拟合的情况，这将会在下一篇文章中讨论。

LogisticRegression() 是自己所写的算法，之所以能直接传入管道使用，因为自己所写的算法遵循了 scikit-learn 的标准——__init__()函数、fit()函数、predict()函数、score()函数等。