学习完二叉树后,为了巩固二叉树的知识、加深对二叉树的理解,故运用 C++ 对各个操作进行实现并用类进行封装,顺便复习了 C++ 的有关知识。虽然在实现的过程中使用了泛型,但是实际使用时只能传入 char,运用泛型只是复习对泛型的运用而已。
//
// main.cpp
// 二叉树类
//
// Created by louyu on 2019/10/26.
// Copyright © 2019 louyu. All rights reserved.
//
#include <bits/stdc++.h>
using namespace std;
template<class T>
struct TriNode {
T data;
struct TriNode* lChild;
struct TriNode* rChild;
TriNode(T data, TriNode<T>* l = NULL,TriNode<T>* r = NULL) {
this->data = data;
lChild = l;
rChild = r;
}
TriNode() {
lChild = rChild = NULL;
}
};
template<class T>
class BinaryTree {
public:
BinaryTree() {
this->pRoot = NULL;
}
//复制构造函数,复制一棵二叉树
BinaryTree(BinaryTree<T> const & c) {
this->pRoot = _copyBinaryTree(c.pRoot);
}
void destoryBinaryTree() {
_destoryBinaryTree(pRoot);
}
//先序生成二叉树,空指针由“#”表示
void preorderCreateBinaryTree(string a) {
int i = 0;
_preorderCreateChildTree(this->pRoot, a, i);
}
//根据先序、中序遍历序列生成二叉树。前提:二叉树中的元素不重复
void preAndInOrderCreateBinaryTree(string a, string b) {
_preAndInOrderCreateBinaryTree(this->pRoot, a, b);
}
//先序递归遍历二叉树
void preorderTransferTree() {
_preorderTransferTree(this->pRoot);
cout<<endl;
}
//中序递归遍历二叉树
void inorderTransferTree() {
_inorderTransferTree(this->pRoot);
cout<<endl;
}
//后序递归遍历二叉树
void postorderTransferTree() {
_postorderTransferTree(this->pRoot);
cout<<endl;
}
//先序非递归遍历二叉树
void preorderTransferTreeNoRecursive() {
stack<TriNode<T>*> s;
TriNode<T>* p;
s.push(this->pRoot); //根指针入栈
while (!s.empty()) {
p = s.top();
while (p) {
cout<<p->data<<" ";
p = p->lChild;
s.push(p); //向左走到尽头
}
s.pop(); //空指针退栈
if (!s.empty()) { //向右一步访问结点
p = s.top();
s.pop();
s.push(p->rChild);
}
}
cout<<endl;
}
//中序非递归遍历二叉树
void inorderTransferTreeNoRecursive() {
stack<TriNode<T>*> s;
TriNode<T>* p;
s.push(this->pRoot); //根指针入栈
while (!s.empty()) {
p = s.top();
while (p) {
p = p->lChild;
s.push(p); //向左走到尽头
}
s.pop(); //空指针退栈
if (!s.empty()) { //向右一步访问结点
p = s.top();
s.pop();
cout<<p->data<<" ";
s.push(p->rChild);
}
}
cout<<endl;
}
//后续非递归遍历二叉树
void postorderTransferTreeNoRecursive() {
stack<TriNode<T>*> s;
TriNode<T>* p, *q = NULL;
s.push(this->pRoot);
while (!s.empty()) {
p = s.top();
while (p) {
p = p->lChild;
s.push(p);
}
s.pop(); //空指针退栈
if (!s.empty()) {
p = s.top();
if (p->rChild)
s.push(p->rChild);
else {
cout<<p->data<<" ";
p = s.top();
s.pop();
if (!s.empty())
q = s.top();
while (q && q->rChild == p) {
cout<<q->data<<" ";
p = q;
s.pop();
q = NULL;
if (!s.empty())
q = s.top();
}
s.push(NULL);
}
}
}
cout<<endl;
}
//运用队列层次遍历二叉树
void levelTraverse() {
queue<TriNode<T>*> q;
if (this->pRoot)
q.push(this->pRoot);
while (!q.empty()) {
TriNode<T>* r;
r = q.front();
q.pop();
cout<<r->data<<" ";
if (r->lChild)
q.push(r->lChild);
if (r->rChild)
q.push(r->rChild);
}
cout<<endl;
}
void clearBinaryTree() {
_destoryBinaryTree(pRoot);
}
//判断是否为空
bool binaryTreeIsEmpty() {
return pRoot == NULL;
}
//求二叉树深度
int depth() {
return _depth(this->pRoot);
}
//返回二叉树中元素值为e结点的指针
TriNode<T>* locate(T e) {
return _locate(this->pRoot, e);
}
//返回特定结点的双亲的指针
TriNode<T>* parent(TriNode<T>*& p) {
return _parent(this->pRoot, p);
}
//返回值为e的结点的左孩子结点指针
TriNode<T>* leftChild(T e) {
TriNode<T>* p = _locate(this->pRoot, e);
if (p)
return p->lChild;
else
return NULL;
}
//返回值为e的结点的右孩子结点指针
TriNode<T>* rightChild(T e) {
TriNode<T>* p = _locate(this->pRoot, e);
if (p)
return p->rChild;
else
return NULL;
}
//返回结点p的左兄弟结点指针
TriNode<T>* leftSibling(TriNode<T>*& p) {
TriNode<T>* father;
father = _parent(this->pRoot, p);
if (father && father->rChild == p)
return father->lChild;
return NULL;
}
TriNode<T>* rightSibling(TriNode<T>*& p) {
TriNode<T>* father;
father = _parent(this->pRoot, p);
if (father && father->lChild == p)
return father->rChild;
return NULL;
}
int countLeaf() {
int n = 0;
_countLeaf(this->pRoot, n);
return n;
}
~BinaryTree() {
_destoryBinaryTree(pRoot);
}
private:
TriNode<T>* pRoot;
void _preorderCreateChildTree(TriNode<T>*& p, string& a, int & i) {
if (a[i] == '#') //#为空指针的标识符
p = NULL;
else {
p = new TriNode<T>(a[i]);
_preorderCreateChildTree(p->lChild, a, ++i);
_preorderCreateChildTree(p->rChild, a, ++i);
}
}
void _preorderTransferTree(TriNode<T>*& p) {
if (p) {
cout<<p->data<<" ";
_preorderTransferTree(p->lChild);
_preorderTransferTree(p->rChild);
}
}
void _inorderTransferTree(TriNode<T>*& p) {
if (p) {
_inorderTransferTree(p->lChild);
cout<<p->data<<" ";
_inorderTransferTree(p->rChild);
}
}
void _postorderTransferTree(TriNode<T>*& p) {
if (p) {
_postorderTransferTree(p->lChild);
_postorderTransferTree(p->rChild);
cout<<p->data<<" ";
}
}
void _destoryBinaryTree(TriNode<T>*& p) {
if (p) {
_destoryBinaryTree(p->lChild);
_destoryBinaryTree(p->rChild);
delete p;
}
p = NULL;
}
//思路来源:https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/solution/python-di-gui-xiang-jie-by-jalan/
void _preAndInOrderCreateBinaryTree(TriNode<T>*& p, string preorder, string inorder) {
if (inorder.size() == 0) p = NULL; //递归终止条件
else {
int mid = 0;
p = new TriNode<T>(preorder[0]);
//因为没有重复元素,所以可以直接根据值来查找根节点在中序遍历中的位置
for (int i = 0; i<inorder.size(); i++) {
if (inorder[i] == preorder[0]) {
mid = i;
break;
}
}
//构建左子树
_preAndInOrderCreateBinaryTree(p->lChild, preorder.substr(1, mid), inorder.substr(0, mid));
//构建右子树
_preAndInOrderCreateBinaryTree(p->rChild, preorder.substr(mid+1), inorder.substr(mid+1));
}
}
int _depth(TriNode<T>* &p) {
if (!p)
return 0;
int hLeft,hRight;
hLeft = _depth(p->lChild);
hRight = _depth(p->rChild);
return hLeft > hRight ? hLeft + 1 : hRight + 1;
}
TriNode<T>* _locate(TriNode<T>*& p, T &e) {
if (!p || p->data == e)
return p;
TriNode<T>* q = NULL;
q = _locate(p->lChild, e);
if (q)
return q;
q = _locate(p->rChild, e);
return q;
}
TriNode<T>* _parent(TriNode<T>*& p, TriNode<T>*& q) {
if (p == NULL || p == q)
return NULL;
if (p->lChild == q || p->rChild == q)
return p;
TriNode<T>* r = NULL;
r = _parent(p->lChild, q);
if (r)
return r;
r = _parent(p->rChild, q);
return r;
}
TriNode<T>* _copyBinaryTree(TriNode<T>*& p) {
if (p == NULL)
return NULL;
else {
TriNode<T>* q;
q = new TriNode<T>(p->data);
q->lChild = copyBinaryTree(p->lChild);
q->rChild = copyBinaryTree(p->rChild);
return q;
}
}
void _countLeaf(TriNode<T>*& p, int & n) {
if (p) {
_countLeaf(p->lChild, n);
_countLeaf(p->rChild, n);
if (!p->lChild && !p->rChild)
n++;
}
}
};
int main() {
BinaryTree<char> tree1;
tree1.preorderCreateBinaryTree("-+a##*b##-c##d##/e##f##");
cout<<tree1.depth()<<endl;
tree1.preorderTransferTree();
tree1.inorderTransferTree();
tree1.postorderTransferTree();
tree1.levelTraverse();
cout<<tree1.countLeaf()<<endl;
cout<<endl;
BinaryTree<char> tree2;
tree2.preAndInOrderCreateBinaryTree("abdefc", "dbefac");
cout<<tree2.depth()<<endl;
tree2.preorderTransferTreeNoRecursive();
tree2.inorderTransferTreeNoRecursive();
tree2.postorderTransferTreeNoRecursive();
tree2.levelTraverse();
cout<<tree2.countLeaf()<<endl;
return 0;
}
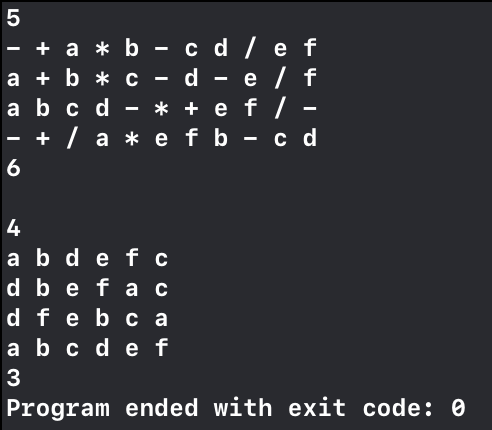
运行结果如下: