机器学习算法笔记(三十四)：使用 SVM 解决回归问题

前两篇文章主要讨论了用 SVM 解决分类问题，本文来讨论一下如何用 SVM 来解决回归问题。

回归问题的本质就是找到一根直线或者曲线，能够最大程度拟合数据点。如何定义拟合，就是不同回归算法的关键，比如线性回归算法定义拟合的方式就是让数据点到预测的直线相应的 MSE 最小。而对于 SVM 来说，对拟合的定义是不同的。

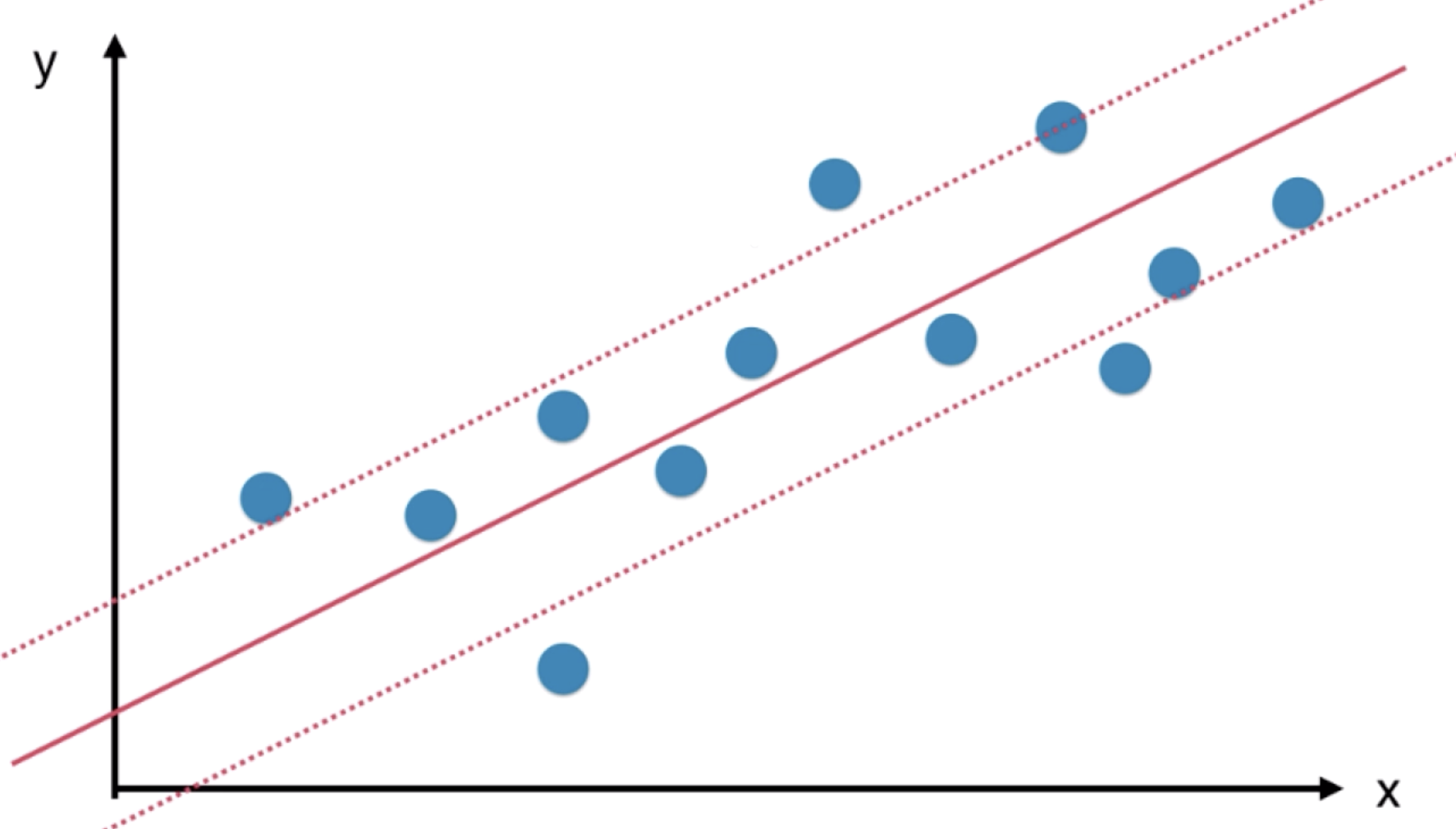
我们需要指定一个所谓的 margin 值，只不过与解决分类问题不同，在 margin 范围内包含的样本数据点越多越好。若在范围内包含的样本越多，那就说明这个范围能比较好的表达样本数据点，此时我们取 margin 中间的直线作为回归预测的结果。

用 SVM解决回归问题的思路与 SVM解决分类问题的思路恰好相反。解决分类问题时，希望 margin区域内没有样本点或者样本点尽可能的少；而解决回归问题时，希望 margin区域内的样本点尽可能多。

在具体训练 SVM 回归问题时，我们对 margin 的范围进行指定，通常引入一个超参数 ε，来指定 margin 上下两根直线中的任意一根直线到中间直线的距离。

对于 SVM 解决回归问题的推导，在《机器学习》一书的第 133 页中有着详细介绍，这里略去。

下面我们使用 sklearn 中封装好的 SVR 类解决回归问题，新建一个工程，创建一个 main.py 文件，实现如下代码：

import numpy as np
from sklearn import datasets

boston = datasets.load_boston()
X = boston.data
y = boston.target

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

from sklearn.svm import SVR

#进行归一化处理
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)

svr = SVR()

from sklearn.model_selection import GridSearchCV
param_grid = [
    {
        'epsilon': np.arange(0, 1, 0.01),
        'C': [i for i in range(1, 200)],
        'kernel': ['poly', 'rbf']
    }
]

grid_search = GridSearchCV(svr, param_grid, n_jobs=-1, verbose=1) #进行对超参数的网格搜索
grid_search.fit(X_standard, y_train)

print(grid_search.best_params_) #打印最佳超参数
best_dt_reg = grid_search.best_estimator_
print(best_dt_reg.score(X_test_standard, y_test))

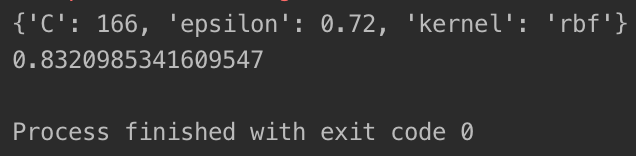
经过数分钟的搜索，打印的网格搜索的结果如下：