机器学习算法笔记(三十二)：支撑向量机(SVM)初探

文章目录

本文开始我们来探讨另一个著名的机器学习算法——支撑向量机(Support Vector Machine，简称 SVM)。使用支撑向量机既可以解决分类问题，也可以解决回归问题，本文就简要讨论一下 SVM 的基础理解与线性 SVM 的实现。

一、什么是支撑向量机

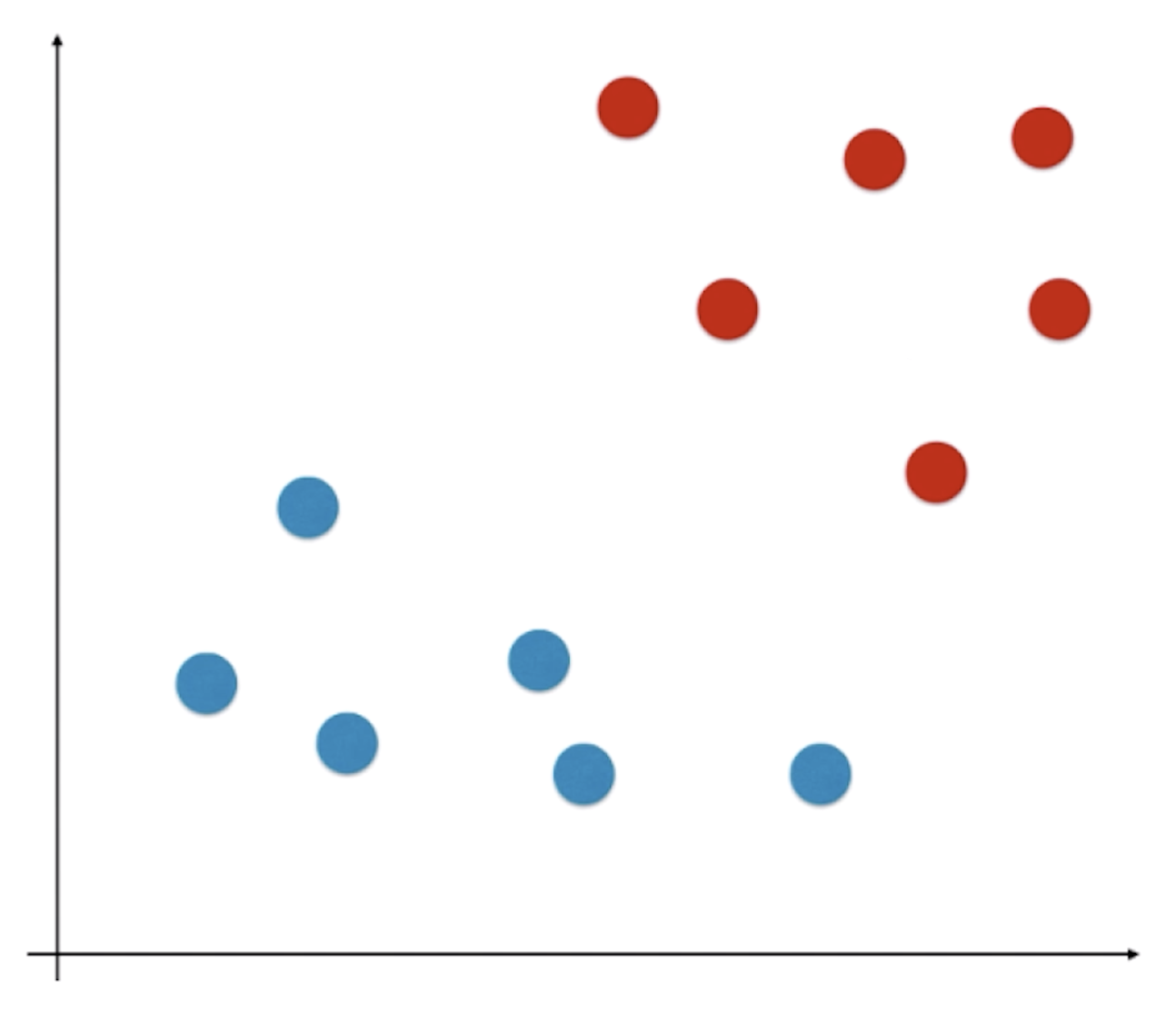
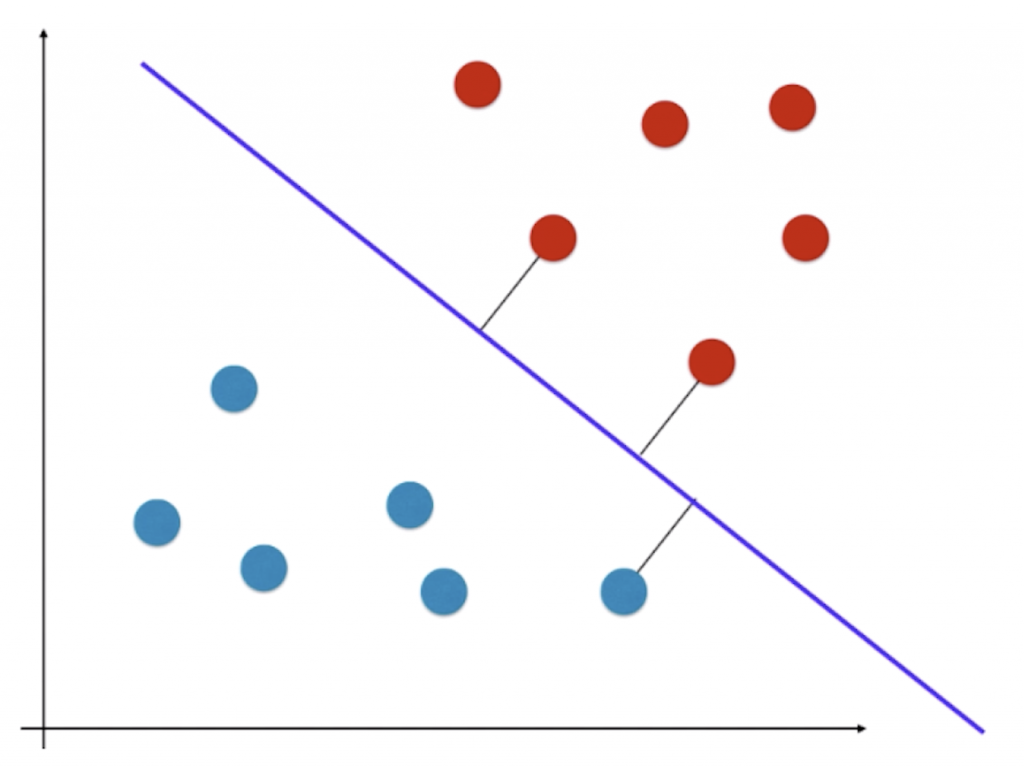
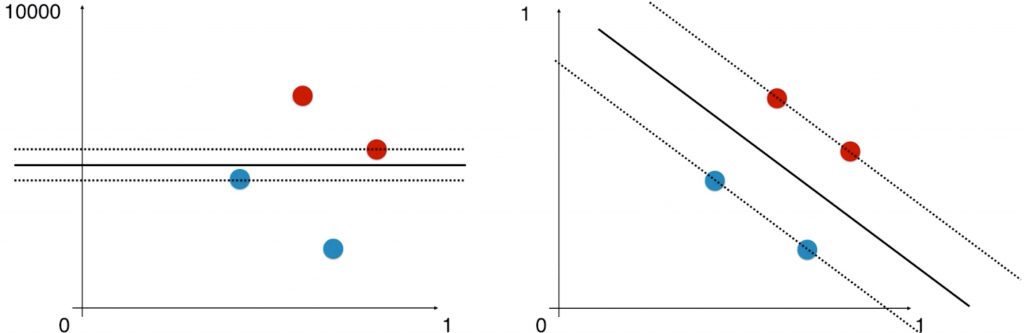
如图所示的特征平面中，所有的特征平面被分成了两类，我们的任务是在这个平面中找到一个决策边界，这个决策边界显然是不唯一的：

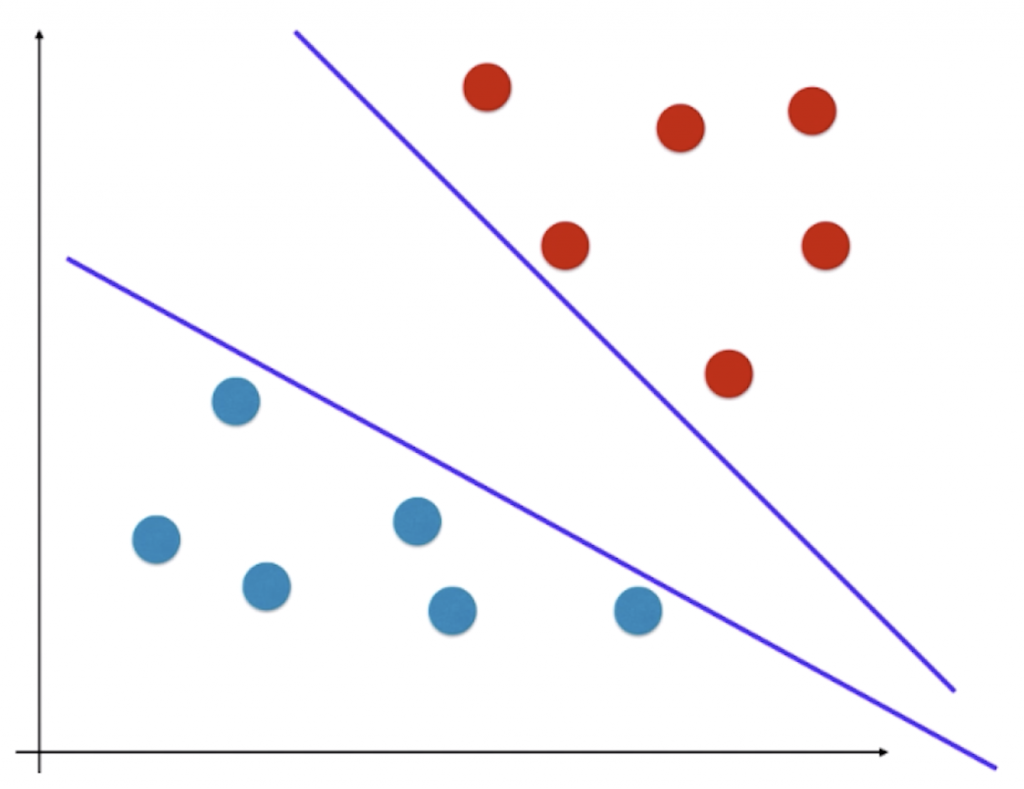
假如我们得到的决策边界是上面那条线，显然该平面在训练数据集上非常好的把训练数据集分成两部分，但是对于机器学习算法来说有一个非常重要的问题——算法的泛化能力。

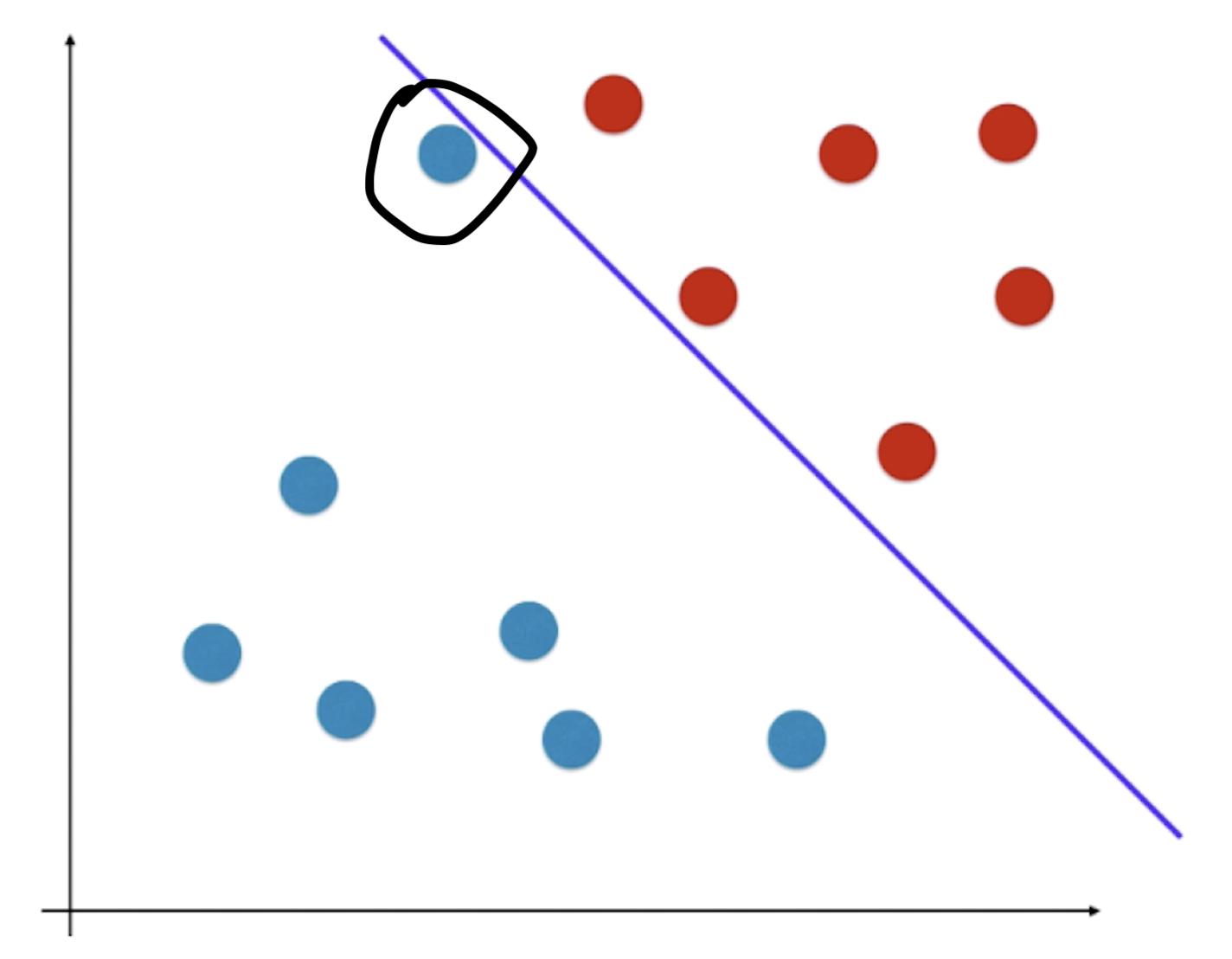
假如某一样本点处于如上图所示的黑圈位置，虽然它被分为蓝色样本，但是我们直观感受它离红色点比较近，很可能其实是一个红色类别的样本。也就是说我们求出的决策边界离红色的点太近了，导致了其它离红色点依然很近的点很可能被分在蓝色类别中。

根据上面的思想，什么样子的决策边界泛化能力比较好呢？在 SVM 中，会考虑让该决策边界离两种类别的样本都尽可能的远（在逻辑回归的决策边界的基础上，让离直线最近的点尽可能的远）。

SVM 在考虑未来模型的泛化能力时，没有寄望在数据的预处理阶段，或者模型的正则化手段上；而是将泛化能力的考量直接放在了算法的内部，找到一条决策边界，决策边界离不同类型的样本都尽可能的远。

为什么离两种类别的样本都尽可能的远的直线，能对该两类样本更好的划分？直观来看，这种决策边界的泛化能力较好，但这种假设不仅仅根据直观的现象，其背后也有数学理论（数学中可以证明，面对 “不适定问题 ”，这种方法找到的决策边界，对应的模型的泛化能力较好）。正是由于这种原因，SVM 也是统计学中重要的方法，其背后有极强的统计理论知识的支撑。

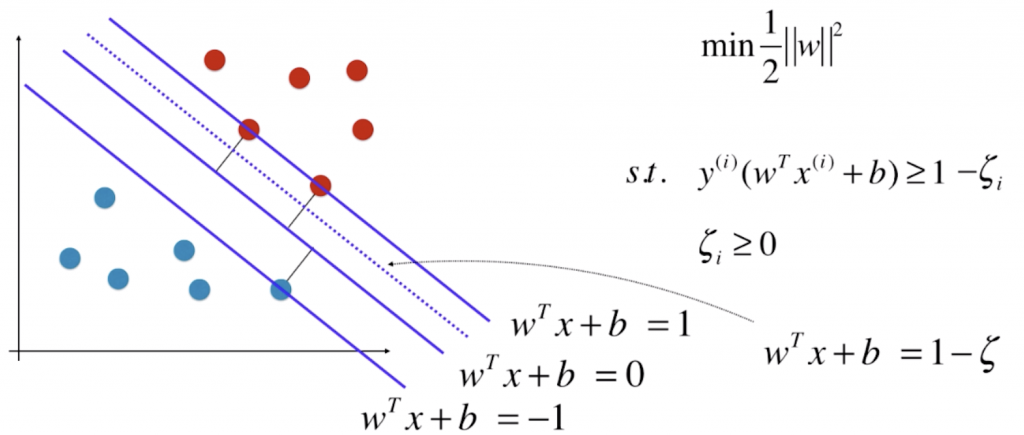
决策边界离不同类型的样本都尽可能远，也就是在这两个类别中，离决策边界最近的点到决策边界的距离尽可能的大。离决策边界最近的这些点又能定义出两条直线，这两条直线与 SVM 的决策边界平行，它们之间将不会有任何的数据点（SVM 的决策边界相当于这片区域最中间的线）。SVM 的任务就是尝试寻找一个最优的决策边界，距离两个类别最近的样本最远，这些样本被称为“支撑向量”。

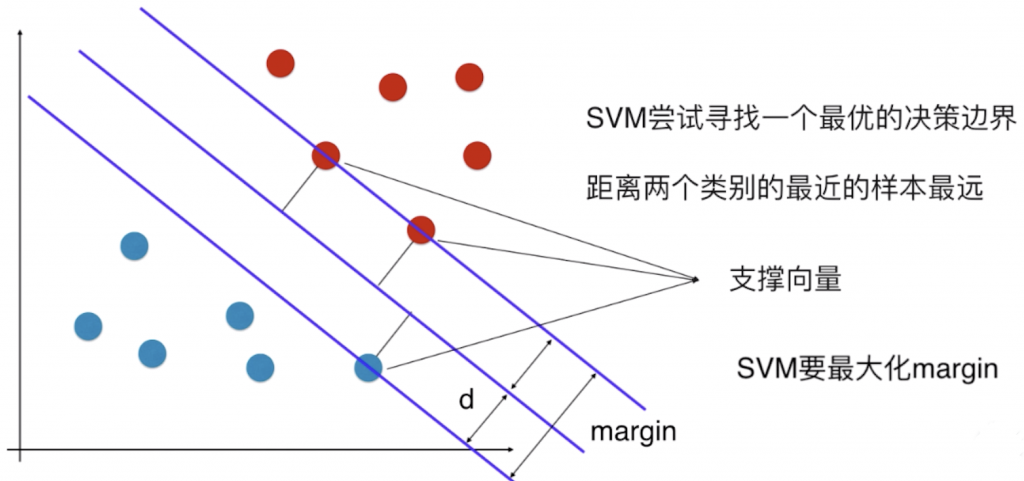
以上讨论的都是线性可分问题，也就是对于特征空间，存在一条直线或一个平面将样本完全分开。这样的算法通常被称为 Hard Margin SVM，这种情况是非常严格的，确实找到了一个决策边界，没有错误的将样本点进行了划分，同时最大化了 margin 的值。相对应的也有 Soft Margin SVM，它用来解决线性不可分的问题，只要在 Hard Margin SVM 上稍加改进即可。

二、SVM 目标函数的推导

SVM 算法的本质就是最大化 margin。因为 margin = 2d，SVM 要最大化 margin，也就是要最大化 d，所以只要找到 d 的表达式，就解决相应的问题了。

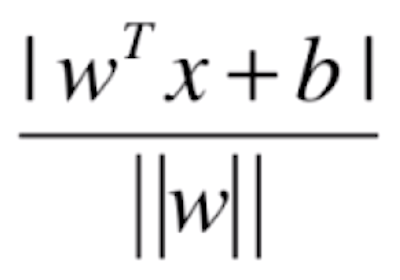在二维平面中，根据高中解析几何知识，平面上一点(x, y)到 Ax+By+C=0 的距离为。拓展到 n 维，直线方程就可以写为的形式，其中 w 向量存放所有样本特征前面的系数（权值），n 维空间的一点 x_b 到的距离为，其中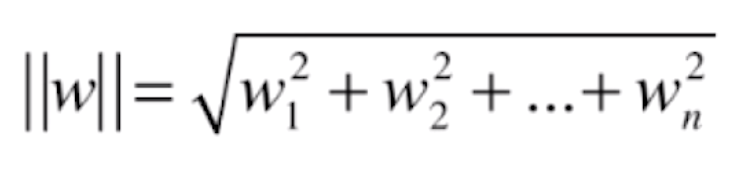。对于 SVM 来说，训练数据集中，所有的样本点到决策边界的距离都大于或等于 d，根据这样的想法，在直线左侧和右侧分两类讨论，就能得到下面的式子：

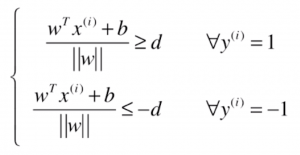
把右边的 d 除到左边去，得：

注意到分母为一个数，那么我们就可以让分子的 w 和 b 除以分母后写为一个字母：

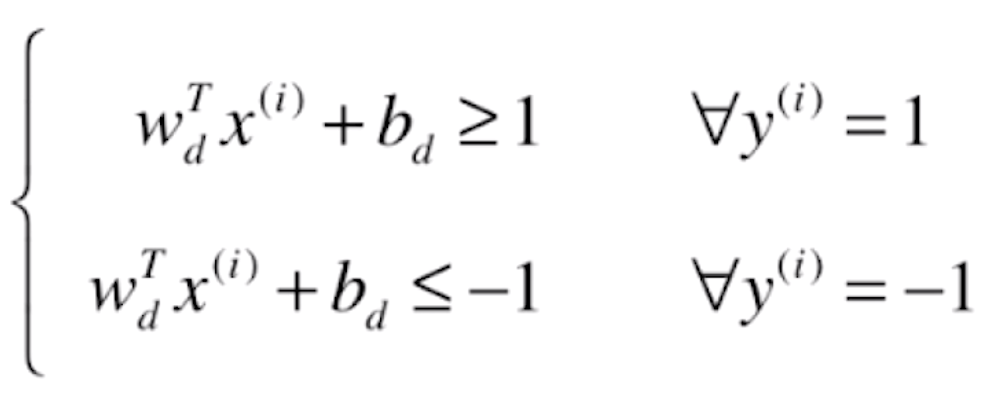
这样我们求得支撑向量组成直线的形式如下：

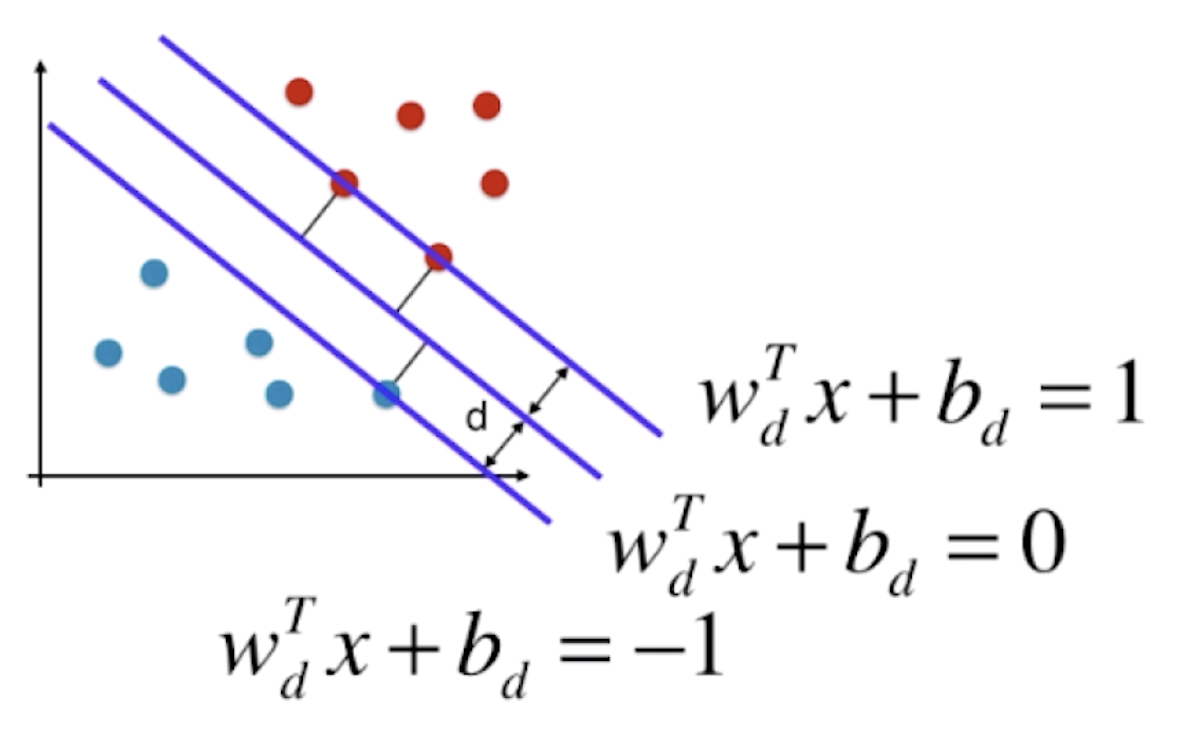
为了方便书写，我们把下标 d 去掉，整个形式如下：

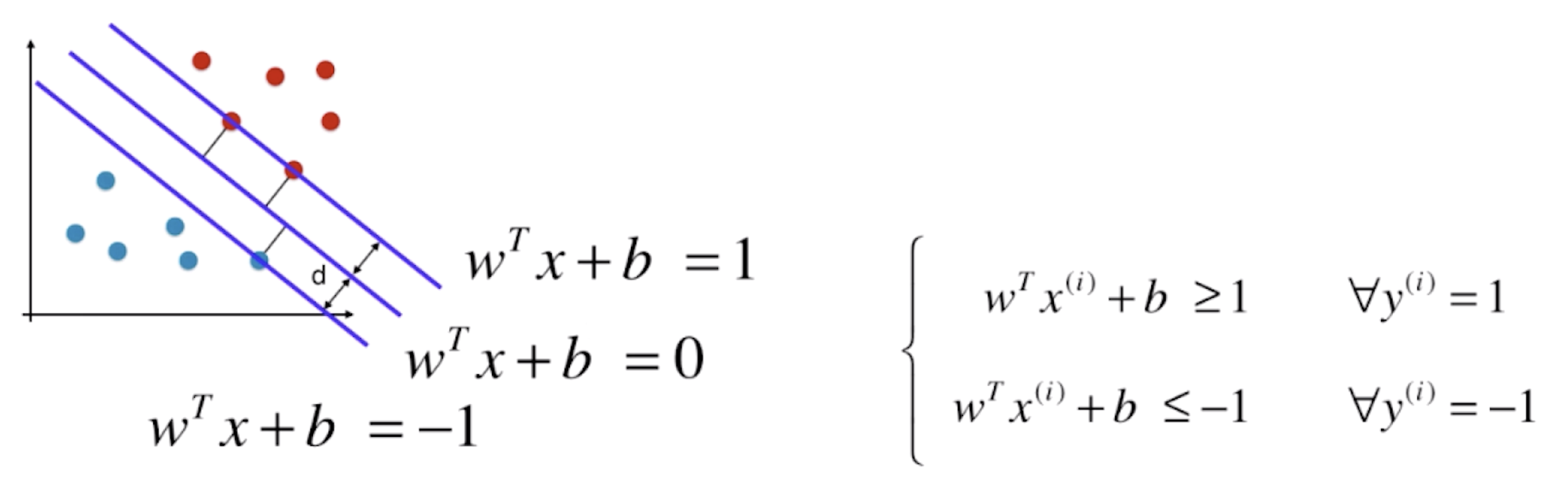
上图中的 w和 b与一开始的 w和 b理论上已经不是一个值了，它们之间相差一个系数关系。

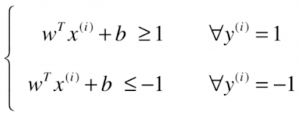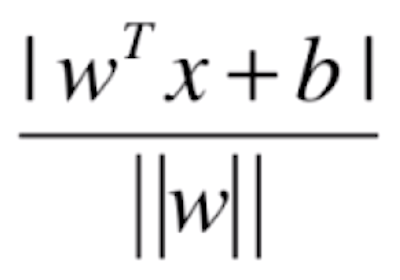对进一步化简，可得。又支撑向量到决策边界的距离为，| w^Tx + b | = 1代入后，我们的目标就变成了最大化，也就相当于最小化，但我们一般写作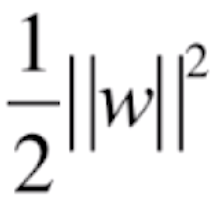，便于进行求导的操作。

综上，我们的 SVM 算法就变成了这样一个最优化问题：最优化的目标函数是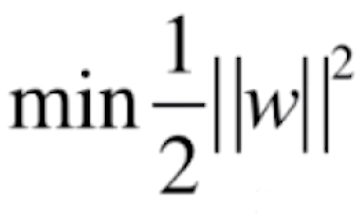，我们需要在限定条件下来最小化目标函数。

这和之前提到的线性回归、逻辑回归不同，它们都是全局最优化问题，只要直接对目标函数求导，让导数等于 0，相应的极值点就有可能是所要求的最大值或者最小值；而 SVM是有条件的最优化问题，求解过程较复杂，需要使用拉格朗日乘数法进行求解。

具体的推导在《统计学习方法(第二版)》的第120页中有详细过程，在这里略去。推导过程中有关对偶问题的储备，可以参考这篇博客或者这篇博客。

三、Soft Margin SVM

上面我们推导了 Hard Margin SVM 相应的最优化问题，但是我们的样本不一定是完全线性可分的，或者有一些特殊的、错误的样本点造成划分出来的决策边界较为极端，这时就需要用到 Soft Margin SVM。

所谓 Soft Margin SVM，就是让 SVM 有容错能力。上节我们提到 SVM 的目标函数是在限定条件下最小化目标函数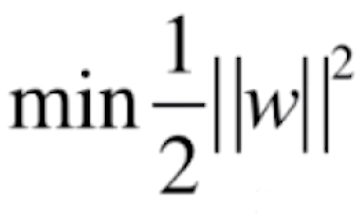。注意限定条件，它的意思是所有的样本点都必须在| w^Tx + b | = 1/-1 这两条直线的外侧。现在对这个条件加以宽松，让所有的数据点不一定在所有区域的外面，也就是给一个宽松量 ζ。

需要注意，ζ 不是一个固定的值，而是每一个样本都有一个相应 ζ_i，也就是说若有 m 个数据点，ζ 也应该有 m 个（对于每一个样本都有一个对应的容错空间）。当然只有这个条件是不够的，我们完全可以让 ζ 趋向于正无穷（虚线在对应直线下面无限远的地方），显然对于所有的数据点都能满足条件，但这个 ζ 明显太大了。ζ 的作用是要求有一定的容错空间，而容错空间又不能太大，此时我们就要在目标函数上加上所有样本对应 ζ 的和，来保证这一点。这样一来，目标函数既反映了 SVM 的思想，又使得 SVM 能容忍一定的错误，这二者之间应该取得一定的平衡。

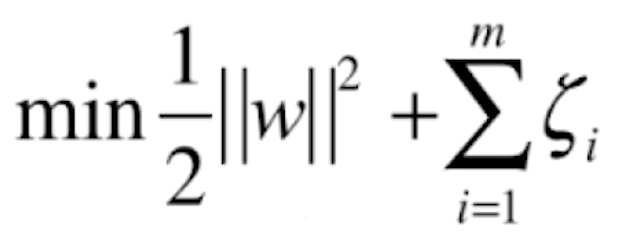
当然，上面那么写代表目标函数中两部分的比例为1:1，也就是同样重要。事实上之前在讨论正则化时，这两部分的比例可以不同，可以在后半部分加上一个参数 C，来平衡这两部分的比例。

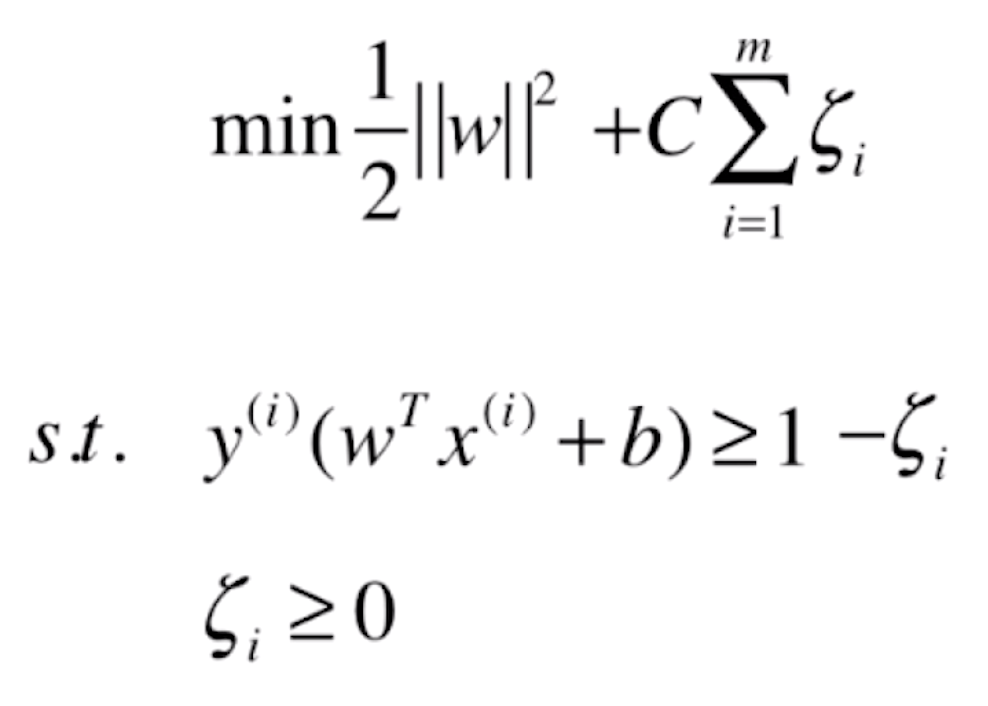
加入参数 C 后的形式，又被称为 Soft Margin SVM 的 L1 正则。

● Soft Margin SVM 也有 L2正则的形式，只不过后面求和的项是 ζ_i的平方和。

● 并不是对于所有的模型添加了正则项都是同样的 L1 范式、L2 范式，对于有些模型，需要改变正则化的策略。但是正则化所要实现的效果是一样的——提升模型的泛化能力。

虽然之前逻辑回归中的参数 C 是放在 MSE 之前的，但 C 在 SVM 中的表意是和之前一样的——C 越大，相应的 ζ 容错空间越小。在 Soft Margin SVM 中，若 C 取正无穷，就代表着我们逼迫这些 ζ_i必须等于零，Soft Margin SVM 就变成了 Hard Margin SVM，也就是容错空间更小。

目前我们讨论的是线性 SVM，至于非线性 SVM我们留到下一篇文章来讨论。

四、使用 sklearn 实现 SVM

在使用 SVM 之前，我们要首先对数据进行归一化处理，因为 SVM 寻找的是使得 margin 最大的区间中间的线，而衡量 margin 的方式是数据点之间的距离，所以 SVM 是涉及距离的。若数据点在不同的维度上的量纲不同，对距离的估计是有问题的。

新建一个工程，创建一个 main.py 文件，实现如下代码：

import numpy as np
import matplotlib.pyplot as plt

from sklearn import datasets

iris = datasets.load_iris()

X = iris.data
y = iris.target

X = X[y<2,:2]
y = y[y<2]

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=666)

#进行归一化处理
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)

#加载SVC，即线性SVM分类器
from sklearn.svm import LinearSVC

svc = LinearSVC(C=1e9) #其中C值就是Soft Margin SVM后一项前面的系数
svc.fit(X_standard, y_train)
print(svc.score(X_test_standard, y_test)) #prints: 1.0

def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])

    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

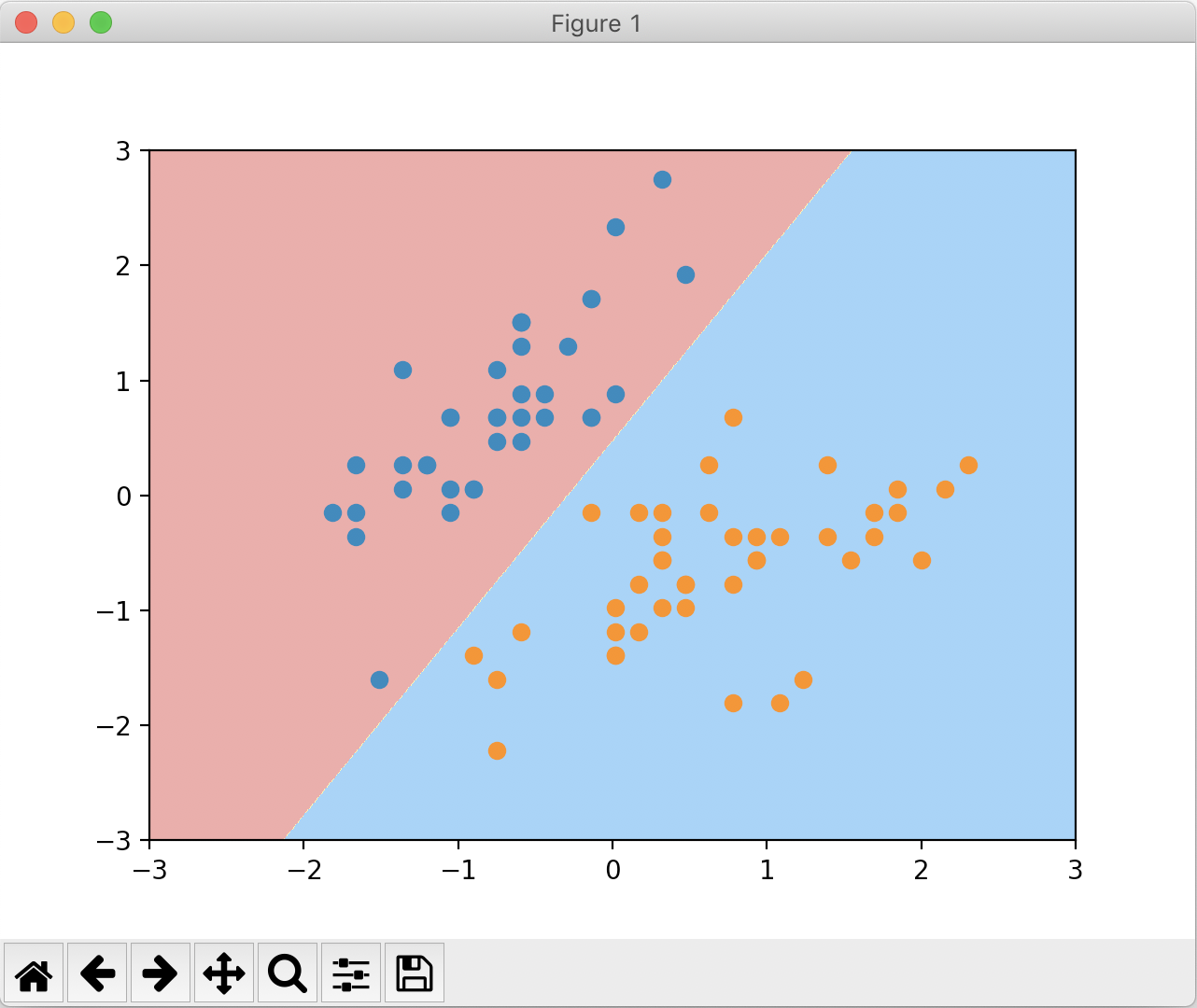
plot_decision_boundary(svc, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[y_train==0,0], X_standard[y_train==0,1])
plt.scatter(X_standard[y_train==1,0], X_standard[y_train==1,1])
plt.show()

绘制的决策边界如下：

我们可以尝试更改 C 为一个较小的值，实现如下：

svc2 = LinearSVC(C=0.01)
svc2.fit(X_standard, y_train)
print(svc2.score(X_test_standard, y_test)) #prints: 1.0

plot_decision_boundary(svc2, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[y_train==0,0], X_standard[y_train==0,1])
plt.scatter(X_standard[y_train==1,0], X_standard[y_train==1,1])
plt.show()

绘制的决策边界如下：

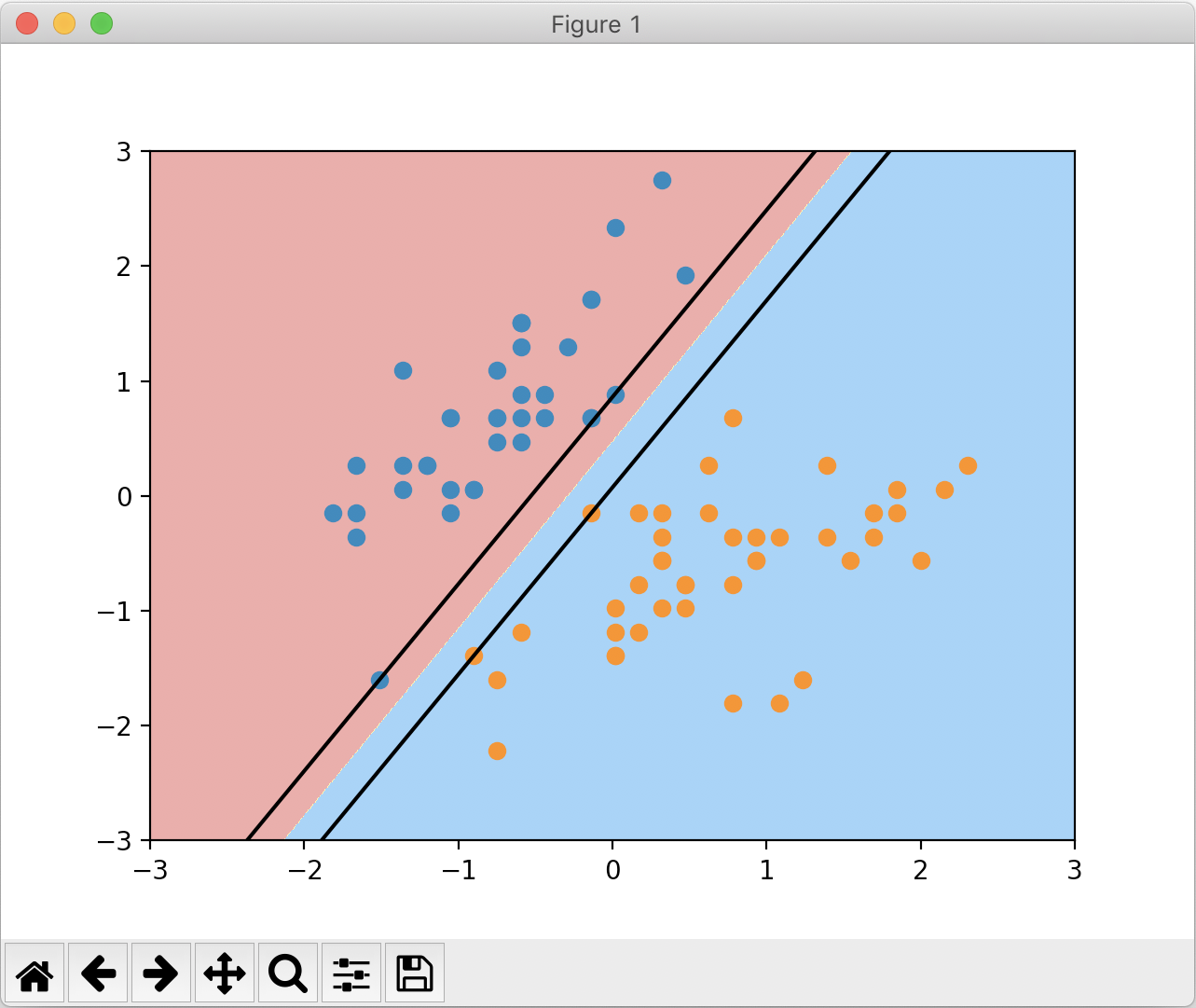
我们还可以绘制出支撑向量所在的直线。修改 plot_decision_boundary 函数为 plot_svc_decision_boundary 如下，并绘制出这两条直线：

def plot_svc_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])

    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

    w = model.coef_[0]
    b = model.intercept_[0]

    # w0*x0 + w1*x1 + b = 0
    # => x1 = -w0/w1 * x0 - b/w1
    plot_x = np.linspace(axis[0], axis[1], 200)
    up_y = -w[0] / w[1] * plot_x - b / w[1] + 1 / w[1]
    down_y = -w[0] / w[1] * plot_x - b / w[1] - 1 / w[1]

    up_index = (up_y >= axis[2]) & (up_y <= axis[3])
    down_index = (down_y >= axis[2]) & (down_y <= axis[3])
    plt.plot(plot_x[up_index], up_y[up_index], color='black')
    plt.plot(plot_x[down_index], down_y[down_index], color='black')

plot_svc_decision_boundary(svc, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[y_train==0,0], X_standard[y_train==0,1])
plt.scatter(X_standard[y_train==1,0], X_standard[y_train==1,1])
plt.show()

绘制结果如下：

打赏赞(1)

一、什么是支撑向量机

二、SVM 目标函数的推导

三、Soft Margin SVM

四、使用 sklearn 实现 SVM

发表回复 取消回复

发表回复取消回复