在第二十和第二十一篇笔记中，我们讨论了两种模型正则化的方式——岭回归(Ridge Regression)与LASSO回归(Least Absolute Shrinkage and Selection Operator Regression)。本文中我们对这两种正则化的方式做一个小小的总结与回顾。
一、L1正则与L2正则
让我们先回到岭回归与LASSO回归的原理：
可以看到，这两种正则化的方法其实就是在MSE后面添加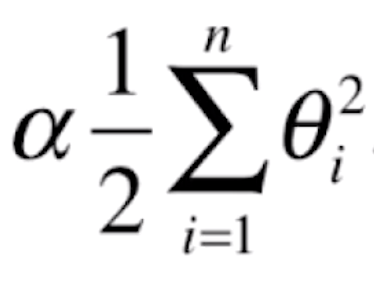
和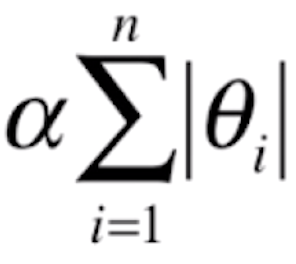
。其实，这两种正则化的表示方式分别与MSE和MAE、欧拉距离和曼哈顿距离的表示是非常像的。
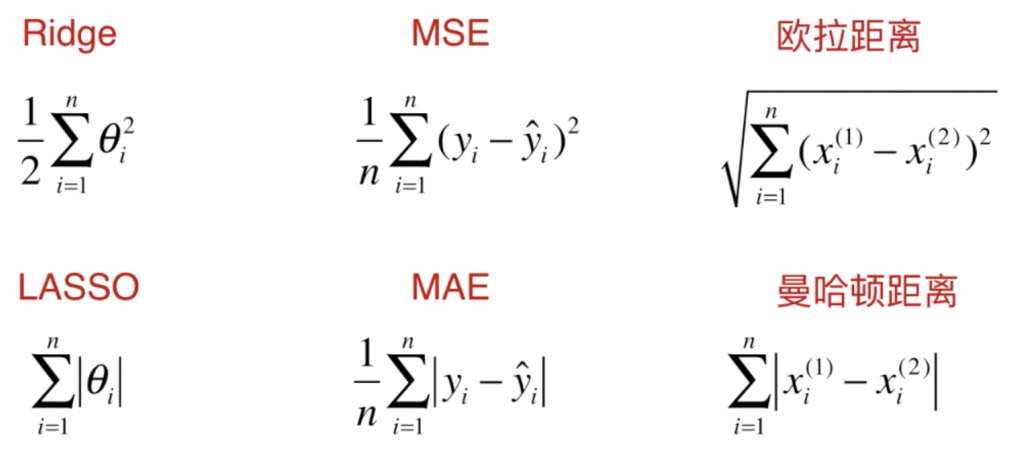
谈到距离，我们知道明科夫斯基距离(Minkowski distance)的表达方式是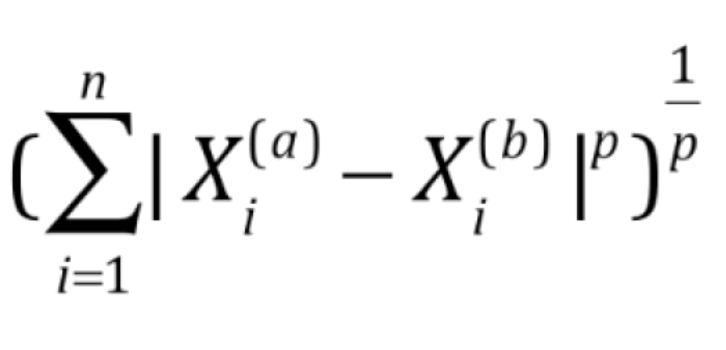
。我们进一步把它提炼泛化，将它变成 Lp 范数
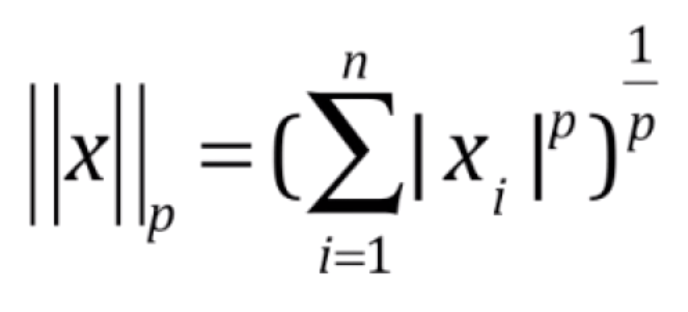的形式。当 p 取1时，其实就是零点到向量 x 的曼哈顿距离；当p取2时，相当于零点到 x 的欧拉距离。结合 Lp 范数的概念，我们就能分别把岭回归和LASSO回归称为 L2 正则项和 L1 正则项。当然理论上也存在 Ln 正则项，但是在实际正则化中，我们一般采用 L1 和 L2 正则项。
这里要特别提一下 L0 正则项。L0 正则项反映了非零的 θ 参数的个数，让 θ 数量尽可能少，进而限制 θ 使得我们得到的曲线不要太陡。然而实际中很少使用 L0 正则来进行模型正则化的过程，而是用 L1 正则代替。
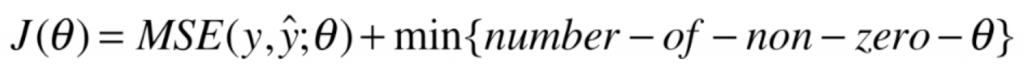
L0正则的优化是一个 NP难的问题。它不能使用诸如梯度下降法，甚至是直接求出一个数学公式这样的方式来直接找到最优解。L0正则项本质是一个离散最优化的问题，可能需要穷举所有的让各种 θ的组合为 0的可能情况，然后依次来计算 J(θ) ，进而来觉得让哪些 θ为 0哪些 θ不为 0，所以说 L0正则的优化是一个 NP难的问题。
二、弹性网
弹性网(Elastic Net)其实背后的意义非常简单。先前提到的岭回归和LASSO回归，都是为MSE添加上一个 L1 或 L2 正则项形成新的损失函数，而弹性网则是结合这两种方式对模型进行正则化：在损失函数后添加 L1 正则项和 L2 正则项。
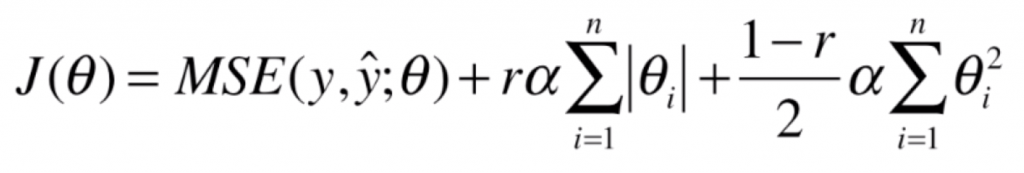
其中，我们引入了一个新的超参数 r，表示添加的两个正则项的比例（分别为 r、1-r ）。我们运用弹性网对模型进行正则化处理，优点在于同时结合了岭回归和 LASSO 回归的优势。
实际应用中，通常在模型正则化时应该先尝试岭回归，因为岭回归的计算是相对精准的。然而岭回归的缺点是，如果特征数量特别多，由于岭回归不具备特征选择功能，不能将某些 θ 化作零，所以当 θ 量太大，可能整体计算量非常大，此时应该优先选择弹性网。这是因为弹性网结合了岭回归计算较为精准的优点，同时又结合了LASSO回归可以进行特征选择的优势。而LASSO回归的缺点在于，它急于将某些 θ 化作零，这个过程可能会产生一些错误（导致特征丢失），使得最终得到的模型偏差比较大。
弹性网结合了岭回归和 LASSO 回归二者的优势，小批量梯度下降法结合了批量梯度下降法和随机批量梯度下降法二者的优势。类似的方法在机器学习领域经常被运用，用来创造出新的方法。
三、模型泛化总结
第十七到第二十一篇笔记讨论了很多模型泛化的问题，训练机器学习模型不是为了在训练集上有着比较好的测试结果，而是为了在面对未来未知的数据下有着比较好的结果。为了让我们的模型有较好的泛化能力，我们讨论了如何看学习曲线、如何进行交叉验证、如何给模型正则化……模型泛化就好比参加考试，参加考试前要做很多练习题备考。这些练习题就相当于训练数据，目的不是为了在做练习题的过程中达到满分，而是通过做练习题让我们在面对考试题时得到更高的分数。考试中面对的新的题目相当于模型在未来生成环境中见到的新的数据。