如果我们在训练模型时把所有的样本数据都当做训练数据的话,这样的模型如果发生了过拟合我们并不自知:因为在这种情况下在训练数据集上的误差会非常小,让我们觉得训练出来的模型很好但很有可能泛化能力不足而出现过拟合。所以对数据集而言要把它分成训练数据集和测试数据集两部分,通过测试数据集来判断模型的好坏。其实在实际应用中,我们通常使用交叉验证(Cross Validation)的方法来训练我们的模型。
一、什么是交叉验证
所谓交叉验证,就是将原始数据集分割为训练数据集和测试数据集,再将训练数据集分割为 k 个数据集,对每一组待调参的超参数,都分别让每一个数据集作为验证数据集,其余数据集一起作为训练数据集,训练出 k 个模型,每一个模型都在对应的验证数据集上求出其性能的指标,k 个模型的性能指标的平均值作为最终衡量该组超参数对应的模型的性能指标。

● 如果最终指标不理想,重新调整参数,再次得到这 k 个模型的性能指标的均值。
● 交叉验证也被称为 k-folds 交叉验证:通常把训练数据集分割为 k 份,每一份都可以称为一个 folds ,因此交叉验证也称为 k-folds 交叉验证。
交叉验证也有着自己的缺点:每次调试一组参数都要训练 k 个模型,相当于整体性能慢了 k 倍。
二、为什么要使用交叉验证
之前我们经常将数据集分成训练数据集和测试数据集,通过训练数据集训练模型,通过测试数据集判断模型的好坏,进而对参数进行调整来获得更好的准确率。但这种方式也带来了一个问题——得到的最佳模型有可能会过拟合了测试数据集(模型过拟合测试数据集后,在测试数据集上表现的准确率会升高),得到的模型的准确率不能反应模型真正的性能。
虽然使用训练数据获得模型,但每次通过测试数据集验证模型的好坏,一旦发现模型不好就重新调整参数再次训练新的模型,这个过程一定程度上是模型在围绕着测试数据集进行调整。也就是说,我们在想办法找到一组参数,这组参数使得我们在训练数据集上获得的模型在测试数据集上效果最好,但是由于测试数据集是已知的,我们相当于在针对这组测试数据集进行调参,那么也有可能出现过拟合的现象,也就是说我们得到的模型针对这组测试数据集过拟合了,使得模型在测试数据集上的表现的准确率比其真正的准确率偏高。并且,如果测试数据集上有极端的数据,过拟合测试数据的模型会不准确。
当然我们也可以像下图一样,在原本训练数据集和测试数据集的基础上新分割一块验证数据集:
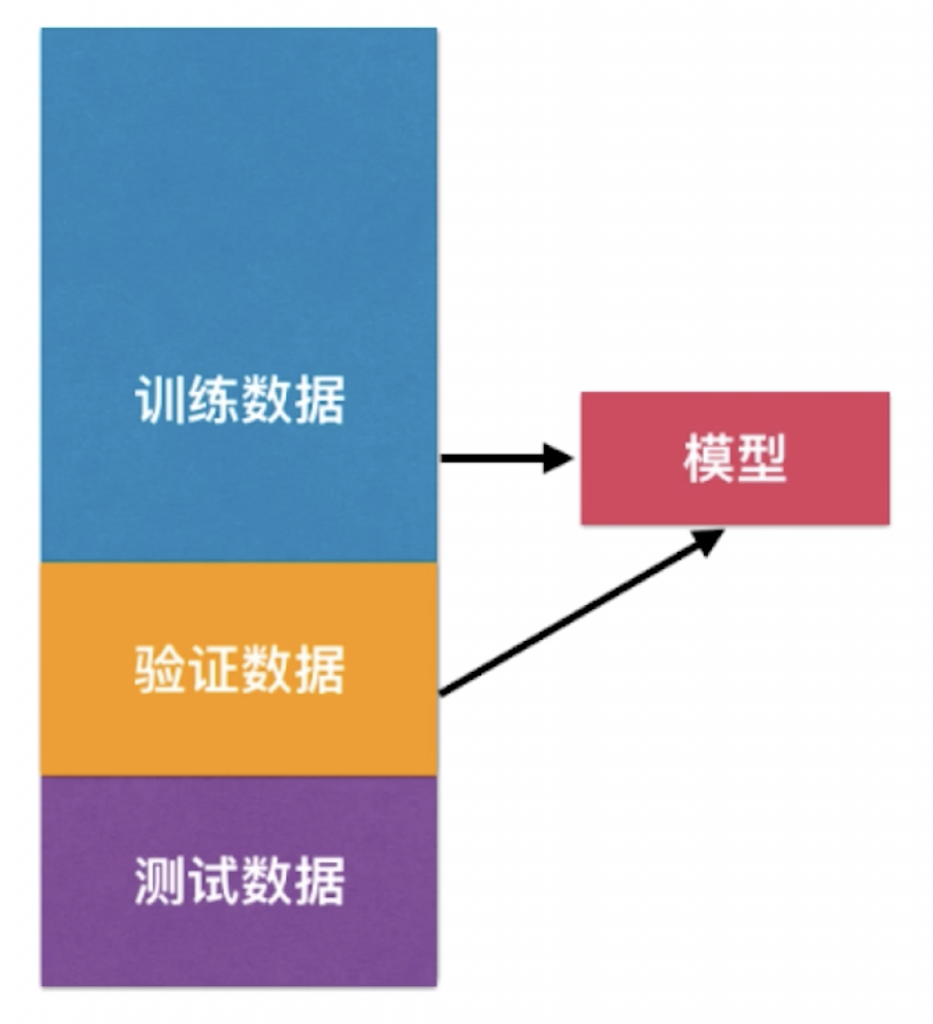
其中,验证数据集用来验证模型的效果。如果模型的效果不好,则重新调整参数再次训练新的模型,直到找到了一组参数,使得整个模型对验证数据集达到最优。之后将测试数据集传入由验证数据集得到的最佳模型,得到模型最终的性能。
● 训练数据集和验证数据集参与了模型的创建:训练数据集用来训练,验证数据集用来评判,一旦评判不好则重新训练。这两种形式都叫参与了模型的创建。
● 测试数据集不参与模型的创建,其相对模型是完全不可知的,相当于是我们在模拟真正的真实环境中我们的模型完全不知道的数据。
尽管这个方法看似解决了只采用训练集和测试集的问题,然而这种方法还是有缺陷的。我们对整个数据集分割方式是随机的,模型有可能过拟合验证数据集,导致所得的模型的性能指标不能反应模型真正的泛化能力。并且“随机”带来的问题是:只有一份验证数据集,一旦验证数据集中有极端的数据就可能导致模型不准确,那么该模型在测试数据集上体现的泛化能力就不能满足实际要求了。
在含有极端数据的数据集上通过验证得到最高准确率的模型是不准确的,因为该模型可能也拟合了部分极端数据。
而交叉验证就解决了我们上述遇到的所有问题。它对于测试集进行随机的分割并且相互验证,一定程度上缓解了极端数据对于模型最终结果的影响,同时,由于我们最终是把 k 个模型的均值作为结果调参,就算是出现了极端数据,对模型的最终影响也是非常有限的。因此,我们今后应该尽可能使用交叉验证来训练模型。
三、编程实现交叉验证
新建一个工程,创建一个main.py文件,实现以下代码:
import numpy as np
from sklearn import datasets
digits = datasets.load_digits()
X = digits.data
y = digits.target
#实现train_test_split作为对照
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=666)
from sklearn.neighbors import KNeighborsClassifier
best_k, best_p, best_score = 0, 0, 0
for k in range(2, 11):
for p in range(1, 6):
knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=k, p=p)
knn_clf.fit(X_train, y_train)
score = knn_clf.score(X_test, y_test)
if score > best_score:
best_k, best_p, best_score = k, p, score
print("Best K =", best_k)
print("Best P =", best_p)
print("Best Score =", best_score)
#实现交叉验证
from sklearn.model_selection import cross_val_score
knn_clf = KNeighborsClassifier()
cross_val_score(knn_clf, X_train, y_train, cv=3) #参数cv代表把训练集分成几份做交叉验证
best_k, best_p, best_score = 0, 0, 0
for k in range(2, 11):
for p in range(1, 6):
knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=k, p=p)
scores = cross_val_score(knn_clf, X_train, y_train)
score = np.mean(scores)
if score > best_score:
best_k, best_p, best_score = k, p, score
print("Best K =", best_k)
print("Best P =", best_p)
print("Best Score =", best_score)
运行结果如下:
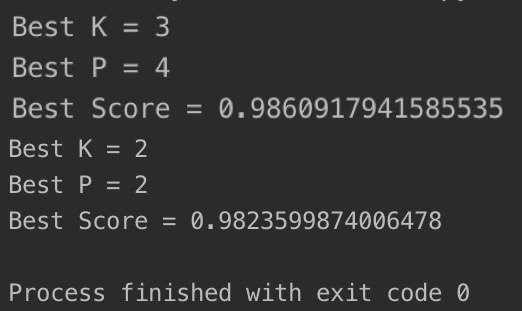
把交叉验证的结果与train_test_split的结果作比较,我们发现,得到的Best K与Best P是不一样的,这种情况我们偏向采用交叉验证得到的参数。因为在train_test_split中得到的参数很有可能只是过拟合了测试数据集而已。同时,我们在交叉验证中得到的分数0.982是低于train_test_split中的分数0.986的。这是因为在交叉验证的过程中,通常不会过拟合某一组的测试数据,所以分数通常会低一些。
我们用交叉验证得到了最好的k和p,那我们的模型最终的准确率就是0.982吗?并不是。交叉验证只是为了拿到最好的k和p而已,拿到这组参数之后,我们就可以获得最佳的分类器了:
best_knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=2, p=2)
best_knn_clf.fit(X_train, y_train)
print(best_knn_clf.score(X_test, y_test)) #prints: 0.980528511821975
最终得到的0.98才是运用交叉验证的方式(更准确的说是三交叉验证)找到的kNN算法的最佳参数组合,此时分类准确度为98%。
X_test和 y_test这两个数据在调参过程中是完全不出现的,对整个模型来说是完全陌生的,我们使用一组模型完全没有见过的数据来测量它最终的准确率,相对来说这个准确率是可以相信的。
四、网格搜索回顾
在先前的文章机器学习算法笔记(二):kNN算法进阶——超参数与网格搜索中,我们其实就接触到了交叉验证。模仿第二篇笔记的内容,在上面的代码下面实现以下代码:
from sklearn.model_selection import GridSearchCV
param_grid = [
{
'weights': ['distance'],
'n_neighbors': [i for i in range(2, 11)],
'p': [i for i in range(1, 6)]
}
]
grid_search = GridSearchCV(knn_clf, param_grid, verbose=1)
grid_search.fit(X_train, y_train)
print(grid_search.best_score_) #和上面的代码一样,这个score并不是最终的准确度,而是交叉验证的准确度
print(grid_search.best_params_)
best_knn_clf = grid_search.best_estimator_
print(best_knn_clf.score(X_test, y_test)) #这才是能代表模型泛化能力的准确度
运行结果如下:

值得补充的是,在极端情况下,k-folds 交叉验证可以变为“留一法”(Leave-One-Out Cross Validation,简称 LOO-CV)的交叉验证方式。具体方式为:设 X_train 有 m 个样本,将 X_train 分割成 m 份,每一个样本作为一份,也就是每次将 m – 1 份样本用于训练,让剩下的一个样本用于测试模型,将 m 次预测结果综合起来进行平均,作为衡量当前参数下这个模型对应的预测准确度。这样做完全不受随机的影响,最接近模型真正的性能指标。很显然这种方法也有着很大的缺点——计算量巨大,训练的时间开销非常大。有些论文中为了研究结果的严谨性,有可能会采用留一法,需要注意。