线性回归法有一个很大的局限性,它要求假设我们数据背后是存在线性关系的。但在实际应用中,具有线性关系假设的数据集相对来说比较少,更多的数据之间具有的是非线性的关系。其实我们用一种非常简单的手段就能改进线性回归法,可以对非线性的数据进行处理和预测,也就是所谓的多项式回归(Polynomial Regression)。
一、什么是多项式回归
线性回归中,对于一些数据,我们想要寻找一条直线,让这一条直线能尽可能的拟合这些数据。
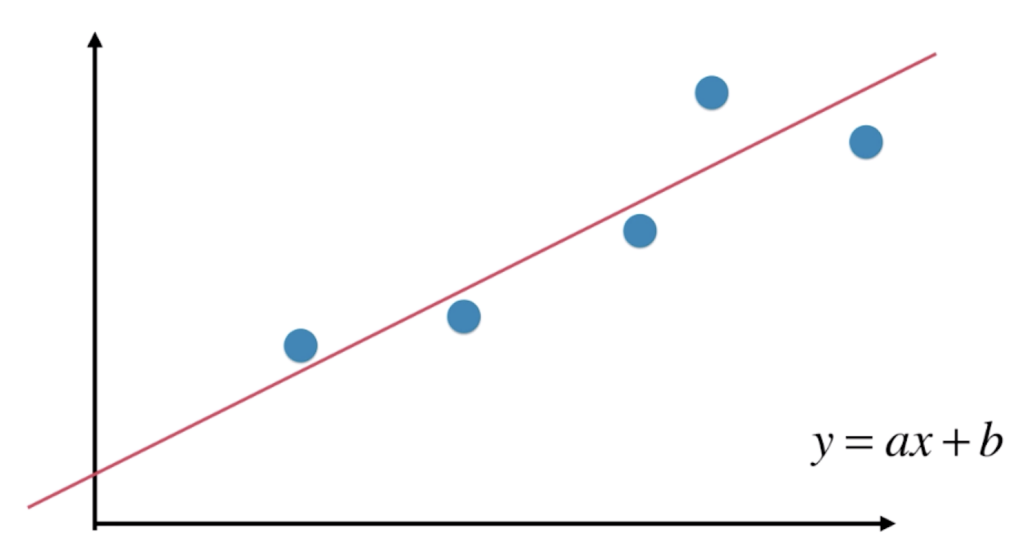
不过对于有一些数据,比如下图的数据,我们当然可以用线性回归法来拟合,但其实它具有非常强的非线性关系,如果我们用二次曲线来拟合这些数据的话,效果会更好:
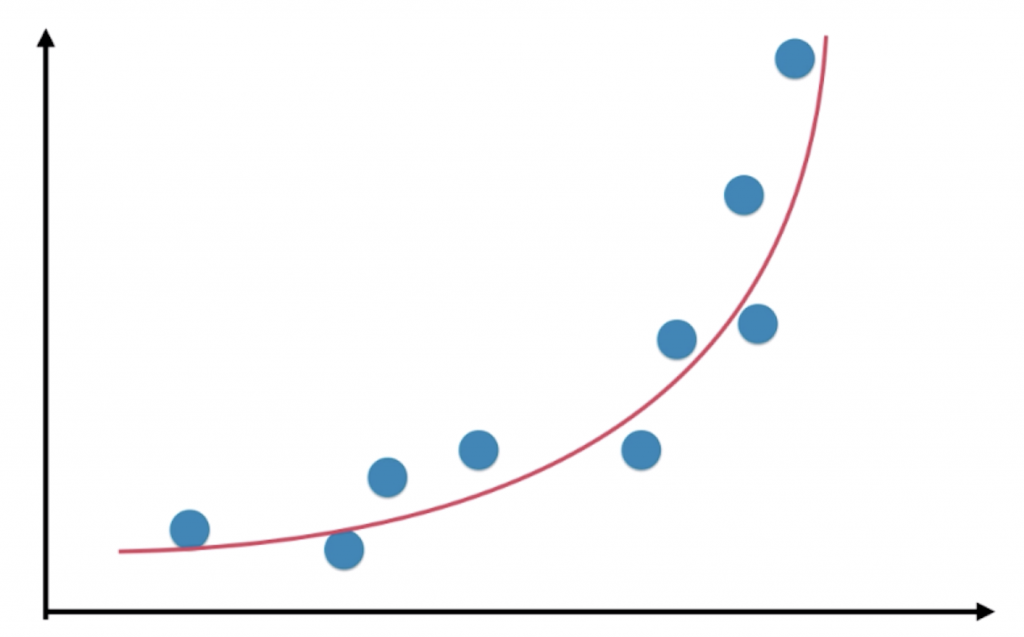
我们就以二次曲线为例,假设所有的样本也只有一个特征,那相应的方程就可以写成 y = ax2 + bx + c 的形式。虽然这个式子是二次的,但我们可以从另外一个角度理解这个式子:我们将 x2 理解成一个特征,x 理解成另外一个特征。换句话说,本来我们的样本只有一个特征 x,现在我把它看做有两个特征这样的一个数据集,多了一个特征就是“ x2 ”。从这个角度理解,y = ax2 + bx + c 依然是一个线性回归的式子,但从 x 的角度看,是一个二次方程,这样的思想就被称为“多项式回归”。
多项式回归相当于为样本多添加了一些特征,这些特征是原来样本的多项式项,比如 x2就是对 x进行平方。增加了这些特征后我们可以使用线性回归的思路更好的拟合原来的数据,但是本质上相当于求出了对于原来的特征而言这种非线性的曲线。
二、编程实现多项式回归
新建一个工程,创建一个main.py文件,实现以下代码:
import numpy as np
import matplotlib.pyplot as plt
#生成测试数据
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)
X2 = np.hstack([X, X**2]) #给数据集添加一个特征,为X中所有数据的平方
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X2, y)
y_predict = lin_reg.predict(X2)
print(lin_reg.coef_) #打印系数
print(lin_reg.intercept_) #打印截距
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()
打印的结果与绘制的图像如下:
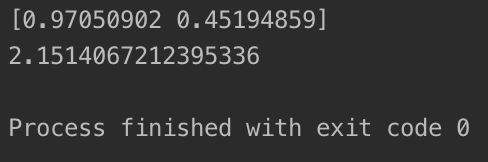
● 打印的系数中,第一个系数是 x的系数,第二个系数是 x2的系数,系数的顺序与我们第 10行中 hstack传参的先后有关。
● 第 22行绘图时,若我们不进行排序,绘制出来的图像会是杂乱的折线,因为 plt是按照给定的坐标顺序绘制折线图。由于测试的数据是随机生成的,不排序就绘制肯定会有问题,需要特别注意。
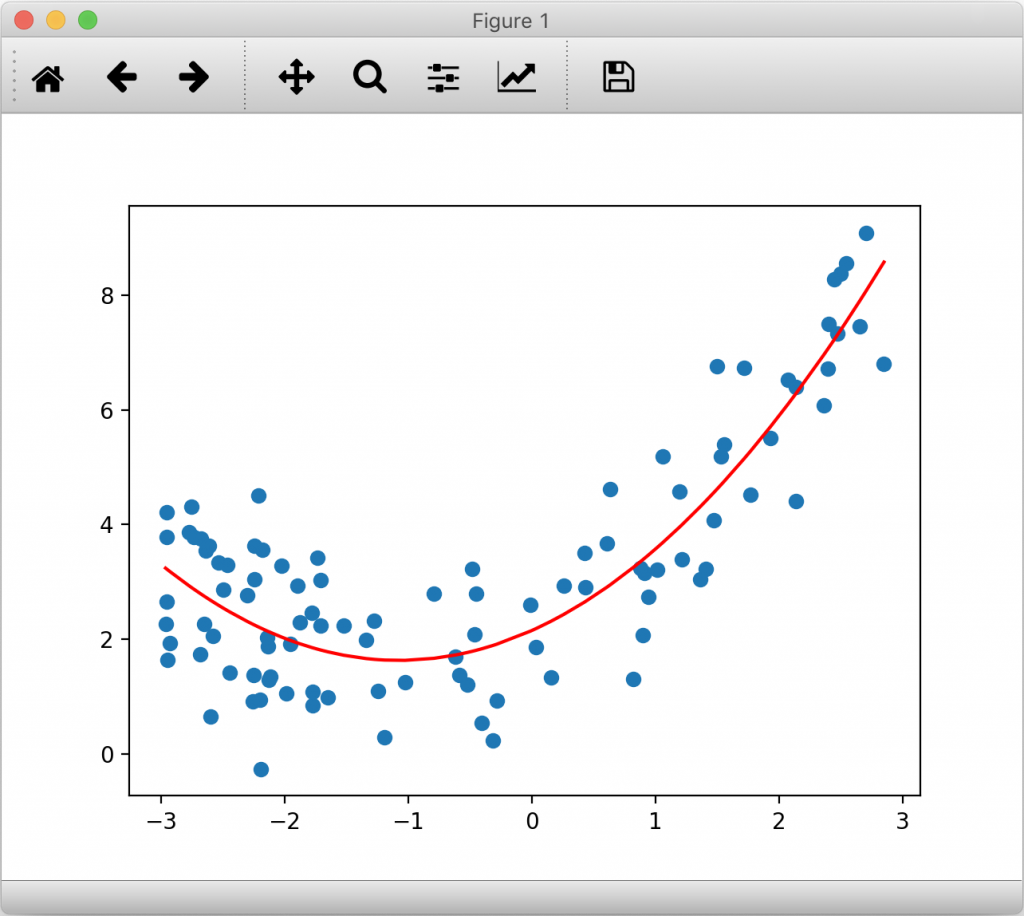
通过上面的实验我们可以看到,多项式回归在算法上完全没有新的地方,完全使用线性回归的思路。它的关键在于我们为原来的数据样本添加新的特征,而我们得到新的特征的方式是原有特征的多项式组合,采用这种方式我们就可以解决非线性问题。与此同时,多项式回归的思路也值得注意。前几篇文章讨论的PCA算法是对数据集进行降维处理,而多项式回归显然在做一件相反的事情:将数据集升维、添加新的特征之后,使得算法更好拟合高维度数据。
三、使用sklearn中的多项式回归
sklearn中多项式回归的调用其实与我们上面提到的相似,只是在对初始数据集添加特征时采用了特定的接口。具体实现如下:
import numpy as np
import matplotlib.pyplot as plt
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)
from sklearn.preprocessing import PolynomialFeatures #加载多项式回归特征构造类
poly = PolynomialFeatures(degree=2) #参数degree代表我们要为原本的数据集最多相应添加几次幂的特征
poly.fit(X)
X2 = poly.transform(X)
print(X[:5,:])
print(X2[:5,:])
from sklearn.linear_model import LinearRegression
lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()
print(lin_reg2.coef_)
print(lin_reg2.intercept_)
其中,第14、15行分别输出了加入特征前后矩阵,输出如下:
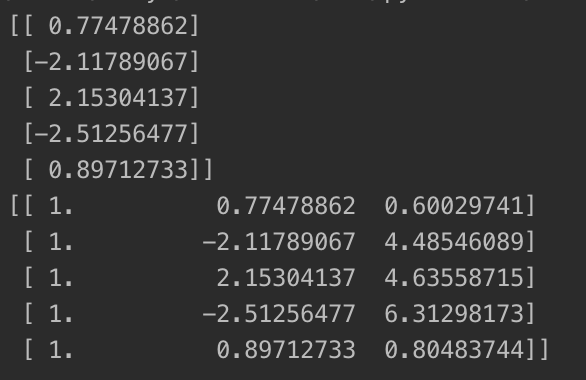
经过处理后,原本只有一列的矩阵变成了三列,其中后两列是原矩阵元素的一次方和平方,第一列全为1,可以看做原矩阵的0次方。
打印的图像和系数、截距分别如下:
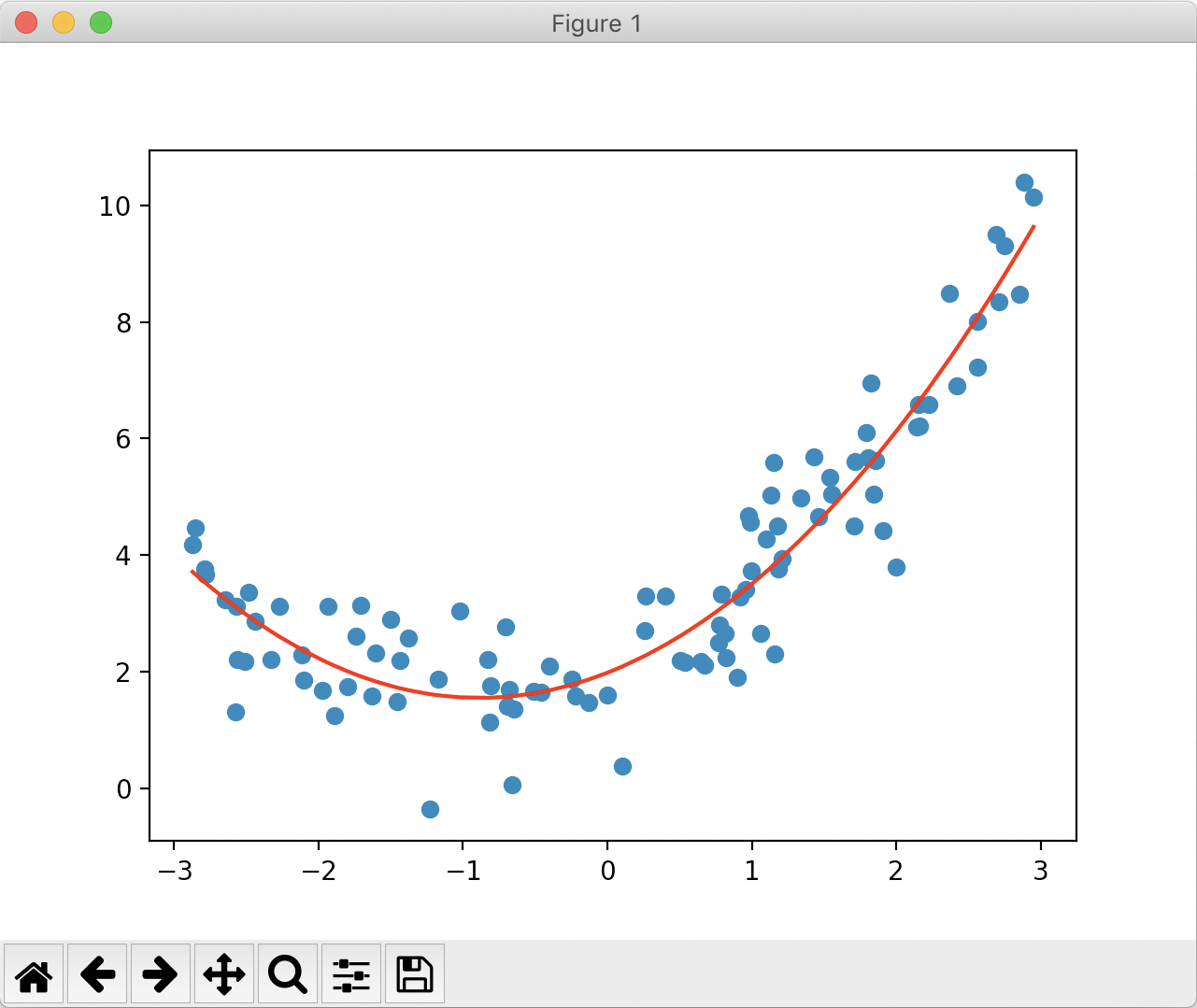

值得一提的是,初始化 PolynomialFeatures时传入的 degree值决定了处理后的矩阵会构造哪些形式。举个例子来说,若一个矩阵为[x, y]( x和 y为常数),且degree为 2,那处理后的矩阵就有[1, x, y, x2, xy, y2]五项(把所有可能的二次及以下形式都构造进去);若传入degree为 3,那么会在[1, x, y, x2, xy, y2]的基础上增加所有三次项的形式,即[1, x, y, x2, xy, y2, x3, y3,xy2 ,x2y]。
四、Pipeline的使用
Pipeline本身是“管道”的意思,在sklearn中,它可以将多项式回归中的三步(多项式特征、数据归一化、线性回归)合在一起,使我们在调用多项式回归时,避免重复调用这三个步骤的麻烦。具体实现如下:
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
#调用Pipeline,传入的是一个列表,列表对应的是"管道"的每一个步骤对应的类
poly_reg = Pipeline([
#传入的是一个元组列表,第一项为该步骤的名字,建议取一个便于辨认的字符串;第二项是这个类的实例
("poly", PolynomialFeatures(degree=2)), #第一步:多项式特征
("std_scaler", StandardScaler()), #第二步:数据归一化
("lin_reg", LinearRegression()) #第三步:线性回归
])
#调用管道使三步合在一起
poly_reg.fit(X, y)
y_predict = poly_reg.predict(X)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()
运行结果应该与分开执行的效果相同。运用Pipeline封装多项式回归能让我们的代码更加简洁,今后我们应尽量用Pipeline来实现多项式回归。