在队列的基本应用:计算k阶斐波那契数列的第n项中,我们讨论了如何运用循环队列来计算k阶斐波那契数列的第n项。在运用循环队列求解时,思路相对来说比较繁琐,不易理解。然而,若我们转换思路采用递归求解,就能够较为轻松地解决问题。
我们知道,k阶斐波那契数列的定义为:前k-1项均为0,第k项为1,以后的每一项都是前k项的和。若我们转换成数学的表达,则有:
f(n)=f(n-1)+f(n-2)+...+f(n-k) ①
将①式两边将n换成n-1,则有:
f(n-1)=f(n-2)+f(n-3)+...+f(n-k-1) (n>k+1) ②
将①式减去②式,易得:
f(n)-f(n-1)=f(n-1)-f(n-k-1) (n>k+1) ③
移项整理得:
f(n)=2f(n-1)-f(n-k-1) (n>k+1) ④
经过简单的数学推导,我们得到了一个k阶斐波那契数列的“递推公式”,这也是我们进行递归的重要依据。需要注意的是,④式n是大于k+1的,所以我们在递归的时候,需要在递归终止条件中加上n=k+1的情况。
#include <bits/stdc++.h>
using namespace std;
int Fibonacci(int k,int n)
{
if (n<=k+1)
{
if (n<=k-1)
return 0;
else
return 1;
}
else
return 2*Fibonacci(k, n-1)-Fibonacci(k, n-k-1);
}
int main()
{
int k,n;
cout<<"请输入斐波那契数列的阶数k:"<<endl;
cin>>k;
cout<<"请输入n的值:"<<endl;
cin>>n;
cout<<k<<"阶斐波那契数列的第"<<n<<"项为"<<Fibonacci(k, n)<<endl;
return 0;
}
我们输入与非递归方法相同的测试数据,运行结果如下:
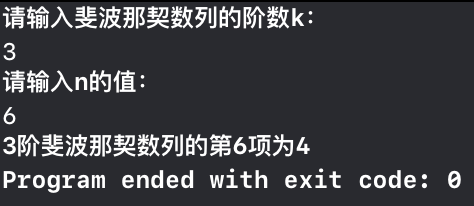
需要注意的是,虽然递归能大大减少代码量以及便于理解,但是其时间复杂度为O(2n),且随着n的增长,需要在栈内分配大量内存,造成了时间与空间的浪费。为了节省时间和空间,我们最好采用循环队列来求解此问题。
前k-1项是0吧
3 , 6 应该是8吧
三阶斐波那契数列是 0, 0, 1, 1, 2, 4…..
第六项为4